初中数学《平行四边形的判定》教案思维导图
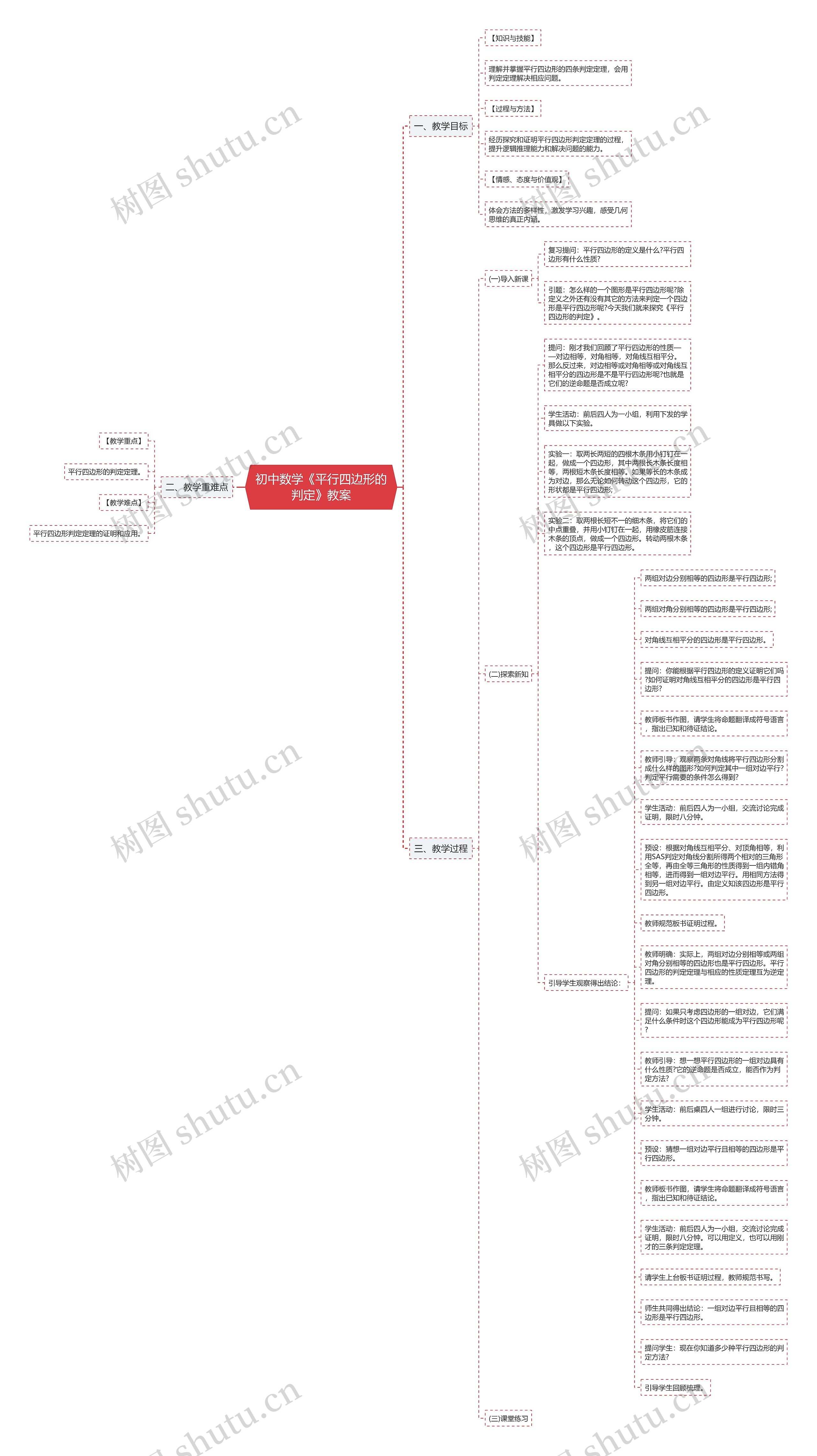
初中数学《平行四边形的判定》教案思维导图重点讲述了平行四边形的判定定理应用,学生需要理解并掌握平行四边形的四条判定定理,经历思考和证明平行四边形判定定理的过程,提升逻辑推理能力和解决问题的能力,激发学习兴趣,感受几何思维的真正内涵。本模板的教学重点在于平行四边形的判定定理,教学难点为平行四边形判定定理的证明和应用,教学过程包含导入新课、探索新知、证明过程,学生需要观察实验结果,思考逆命题,进行证明。除了对角线互相平分的四边形,两组对边分别相等或两组对角分别相等的四边形也是平行四边形,平行四边形的判定定理与相应的性质定理互为逆定理。
思维导图大纲
初中数学《平行四边形的判定》教案思维导图模板大纲
一、教学目标
【知识与技能】
理解并掌握平行四边形的四条判定定理,会用判定定理解决相应问题。
【过程与方法】
经历探究和证明平行四边形判定定理的过程,提升逻辑推理能力和解决问题的能力。
【情感、态度与价值观】
体会方法的多样性,激发学习兴趣,感受几何思维的真正内涵。
二、教学重难点
【教学重点】
平行四边形的判定定理。
【教学难点】
平行四边形判定定理的证明和应用。
三、教学过程
(一)导入新课
复习提问:平行四边形的定义是什么?平行四边形有什么性质?
引题:怎么样的一个图形是平行四边形呢?除定义之外还有没有其它的方法来判定一个四边形是平行四边形呢?今天我们就来探究《平行四边形的判定》。
(二)探索新知
提问:刚才我们回顾了平行四边形的性质——对边相等,对角相等,对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?也就是它们的逆命题是否成立呢?
学生活动:前后四人为一小组,利用下发的学具做以下实验。
实验一:取两长两短的四根木条用小钉钉在一起,做成一个四边形,其中两根长木条长度相等,两根短木条长度相等。如果等长的木条成为对边,那么无论如何转动这个四边形,它的形状都是平行四边形;
实验二:取两根长短不一的细木条,将它们的中点重叠,并用小钉钉在一起,用橡皮筋连接木条的顶点,做成一个四边形。转动两根木条,这个四边形是平行四边形。
引导学生观察得出结论:
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形。
提问:你能根据平行四边形的定义证明它们吗?如何证明对角线互相平分的四边形是平行四边形?
教师板书作图,请学生将命题翻译成符号语言,指出已知和待证结论。
教师引导:观察两条对角线将平行四边形分割成什么样的图形?如何判定其中一组对边平行?判定平行需要的条件怎么得到?
学生活动:前后四人为一小组,交流讨论完成证明,限时八分钟。
预设:根据对角线互相平分、对顶角相等,利用SAS判定对角线分割所得两个相对的三角形全等,再由全等三角形的性质得到一组内错角相等,进而得到一组对边平行。用相同方法得到另一组对边平行。由定义知该四边形是平行四边形。
教师规范板书证明过程。
教师明确:实际上,两组对边分别相等或两组对角分别相等的四边形也是平行四边形。平行四边形的判定定理与相应的性质定理互为逆定理。
提问:如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
教师引导:想一想平行四边形的一组对边具有什么性质?它的逆命题是否成立,能否作为判定方法?
学生活动:前后桌四人一组进行讨论,限时三分钟。
预设:猜想一组对边平行且相等的四边形是平行四边形。
教师板书作图,请学生将命题翻译成符号语言,指出已知和待证结论。
学生活动:前后四人为一小组,交流讨论完成证明,限时八分钟。可以用定义,也可以用刚才的三条判定定理。
请学生上台板书证明过程,教师规范书写。
师生共同得出结论:一组对边平行且相等的四边形是平行四边形。
提问学生:现在你知道多少种平行四边形的判定方法?
引导学生回顾梳理。
(三)课堂练习
相关思维导图模板


树图思维导图提供 初中数学优秀教案大全 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学优秀教案大全 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:551ee80b2009950fd7c88f5eadc7a61d

树图思维导图提供 初中八年级数学上册教案例文 在线思维导图免费制作,点击“编辑”按钮,可对 初中八年级数学上册教案例文 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9058ee3ec768a6f40c3dc99958890f17










 上海工商
上海工商