六年级数学上册各单元思维导图
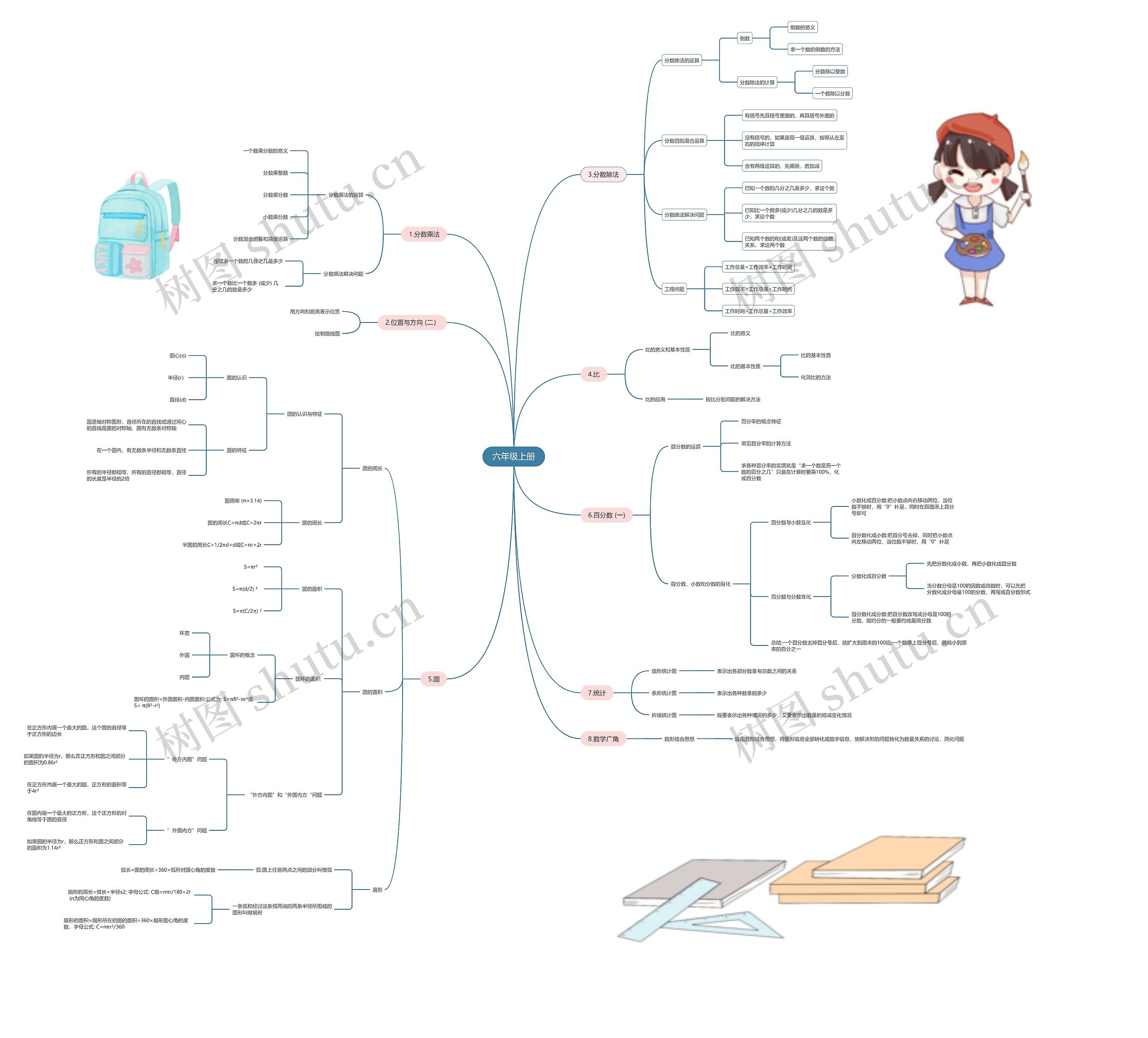
模板展示了六年级数学上册各单元的思维导图,包含分数乘法、位置与方向、圆、分数除法、比、百分数和统计,分数乘法介绍了运算、意义和解决问题的方法,位置与方向则是通过方向和距离表示位置,并绘制路线图,圆的特征包含圆心、半径、直径和对称性,同时介绍了圆的周长和面积的计算方法,和圆环和扇形的概念,分数除法介绍了倒数的意义和方法、四则混合运算和应用于工程问题,比的基本性质和应用,百分数的运算和互化,和扇形、条形和折线统计图的绘制方法,介绍了数形结合思想的应用。
思维导图大纲
六年级上册思维导图模板大纲
1.分数乘法
分数乘法的运算
一个数乘分数的意义
分数乘整数
分数乘分数
小数乘分数
分数混合运算和简便运算
分数乘法解决问题
连续求一个数的几分之几是多少
求一个数比一个数多 (或少) 几分之几的数是多少
2.位置与方向 (二)
用方向和距离表示位置
绘制路线图
5.圆
圆的周长
圆的认识与特征
圆的认识
圆心(o)
半径(r)
直径(d)
圆的特征
圆是轴对称图形,直径所在的直线或通过同心 的直线是圆的对称轴,圆有无数条对称轴
在一个圆内,有无数条半径和无数条直径
所有的半径都相等,所有的直径都相等,直径 的长度是半径的2倍
圆的周长
圆周率 (π≈3.14)
圆的周长C=πd或C=2πr
半圆的周长C=1/2πd+d或C=πr+2r
圆的面积
圆的面积
S=πr²
S=π(d/2) ²
S=π(C/2π) ²
圆环的面积
圆环的概念
环宽
外圆
内圆
圆环的面积=外圆面积-内圆面积;公式为: S=πR²-πr²或 S= π(R²-r²)
“外方内圆”和“外圆内方“问题
”外方内圆”问题
在正方形内画一个最大的圆,这个圆的直径等 于正方形的边长
如果圆的半径为r,那么在正方形和圆之间部分的面积为0.86r²
在正方形内画一个最大的圆,正方形的面积等 于4r²
”外圆内方”问题
在圆内画一个最大的正方形,这个正方形的对 角线等于圆的直径
如果圆的半径为r,那么正方形和圆之间部分的面积为1.14r²
扇形
弧:圆上任意两点之间的部分叫做弧
弧长=圆的周长÷360×弧所对圆心角的度数
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形
扇形的周长=弧长+半径x2; 字母公式: C扇=nπr/180+2r (n为同心角的度数)
扇形的面积=扇形所在的圆的面积÷360×扇形圆心角的度数,字母公式: C=nπr²/360
3.分数除法
分数除法的运算
倒数
倒数的意义
求一个数的倒数的方法
分数除法的计算
分数除以整数
一个数除以分数
分数四则混合运算
有括号先算括号里面的,再算括号外面的
没有括号的,如果是同一级运算,按照从左至右的顺序计算
含有两级运算的,先乘除,后加减
分数除法解决问题
已知一个数的几分之几是多少,求这个数
已知比一个数多(或少)几分之几的数是多少,求这个数
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
工程问题
工作总量=工作效率×工作时间
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
4.比
比的意义和基本性质
比的意义
比的基本性质
比的基本性质
化简比的方法
比的应用
按比分配问题的解决方法
6.百分数 (一)
百分数的运算
百分率的概念特征
常见百分率的计算方法
求各种百分率的实质就是“求一个数是另一个数的百分之几”只是在计算时要乘100%,化成百分数
百分数、小数和分数的互化
百分数与小数互化
小数化成百分数:把小数点向右移动两位,当位数不够时,用“0”补足,同时在后面添上百分号即可
百分数化成小数:把百分号去掉,同时把小数点向左移动两位,当位数不够时,用“0”补足
百分数与分数互化
分数化成百分数
先把分数化成小数,再把小数化成百分数
当分数分母是100的因数或倍数时,可以先把 分数化成分母是100的分数,再写成百分数形式
百分数化成分数:把百分数改写成分母是100的分数,能约分的一般要约成最简分数
总结:一个百分数去掉百分号后,就扩大到原来的100倍;一个数添上百分号后,就缩小到原来的百分之一
7.统计
扇形统计图
表示出各部分数量与总数之间的关系
条形统计图
表示出各种数量的多少
折线统计图
既要表示出各种情况的多少,又要表示出数量的增减变化情况
8.数学广角
数形结合思想
应用数形结合思想,将图形信息全部转化成数字信息,使解决形的问题转化为数量关系的讨论,简化问题
思维导图模板大纲
思维导图模板大纲
思维导图模板大纲
相关思维导图模板

树图思维导图提供 小学数学六年级上册第四单元《比》课堂笔记 在线思维导图免费制作,点击“编辑”按钮,可对 小学数学六年级上册第四单元《比》课堂笔记 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4bb04ae75f82becf6ab609ef988a9a8d
树图思维导图提供 小学数学六年级上册第八单元《数学广角——数与形》课堂笔记 在线思维导图免费制作,点击“编辑”按钮,可对 小学数学六年级上册第八单元《数学广角——数与形》课堂笔记 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d058e483ff68d9455104199af7749b01















 上海工商
上海工商