考研数学7大难点梳理思维导图

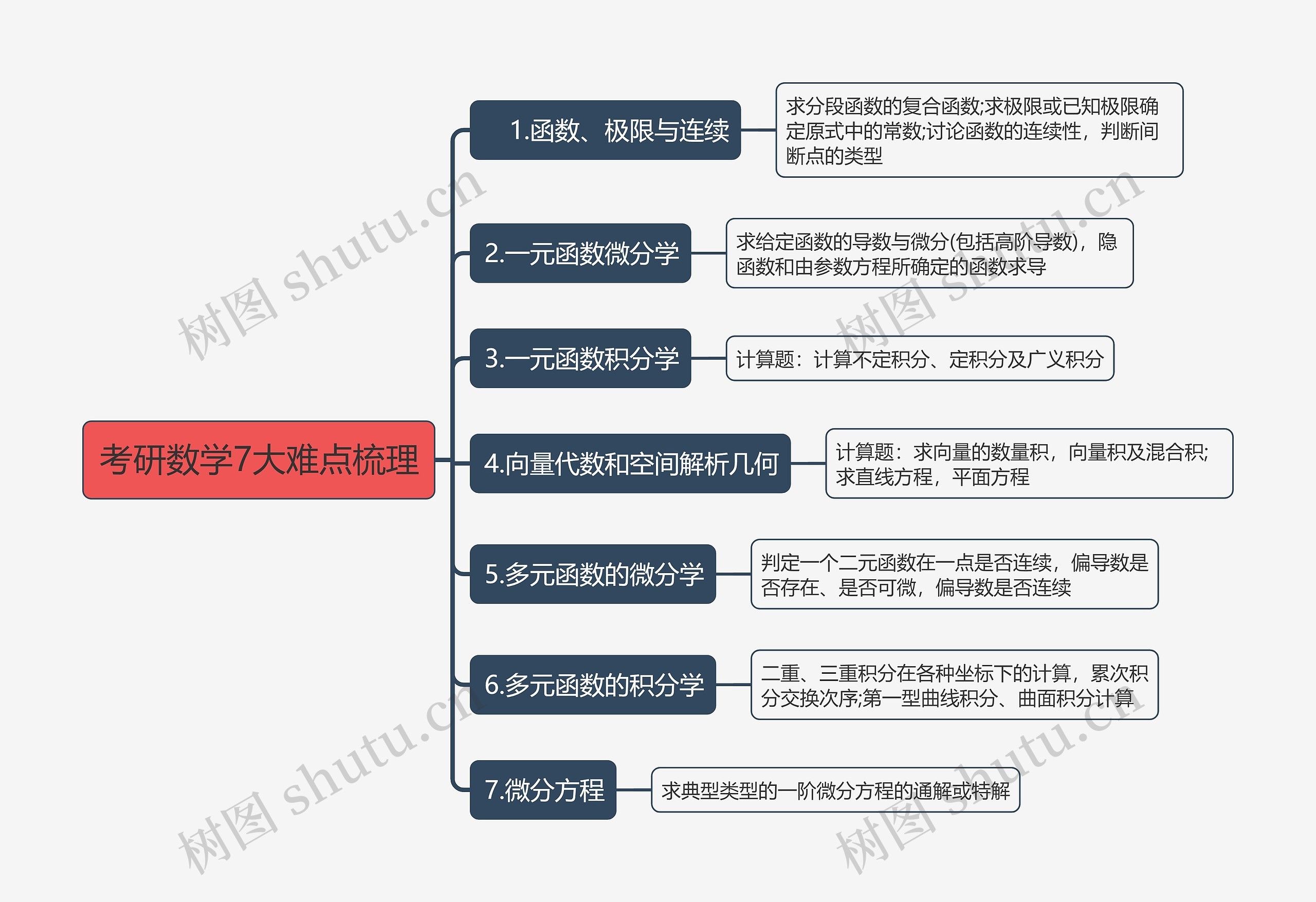
考研数学的难点分为七个大类，包含函数、极限与连续、一元函数微分学、一元函数积分学、向量代数和空间解析几何、多元函数的微分学、多元函数的积分学和微分方程。在函数、极限与连续部分，需要学会求分段函数的复合函数、求极限、确定原函数中的常数和讨论函数的连续性，在一元函数微分学中，需要掌握求导数、微分和高阶导数，和隐函数和由参数方程所确定的函数的求导。在一元函数积分学方面，需要计算类型的积分问题。向量代数和空间解析几何部分，需要求解向量的数量积、向量积及混合积，和求解直线和平面的方程，在多元函数的微分学方面，需要判定二元函数在一点是否连续，偏导数是否存在、是否可微和偏导数是否连续。在多元函数的积分学中，需要掌握二重、三重积分各种坐标下的计算和累次积分交换次序，还需要计算第一型曲线积分和曲面积分，在微分方程部分，需要求解典型类型的一阶微分方程的通解或特解。