无穷级数思维脑图思维导图
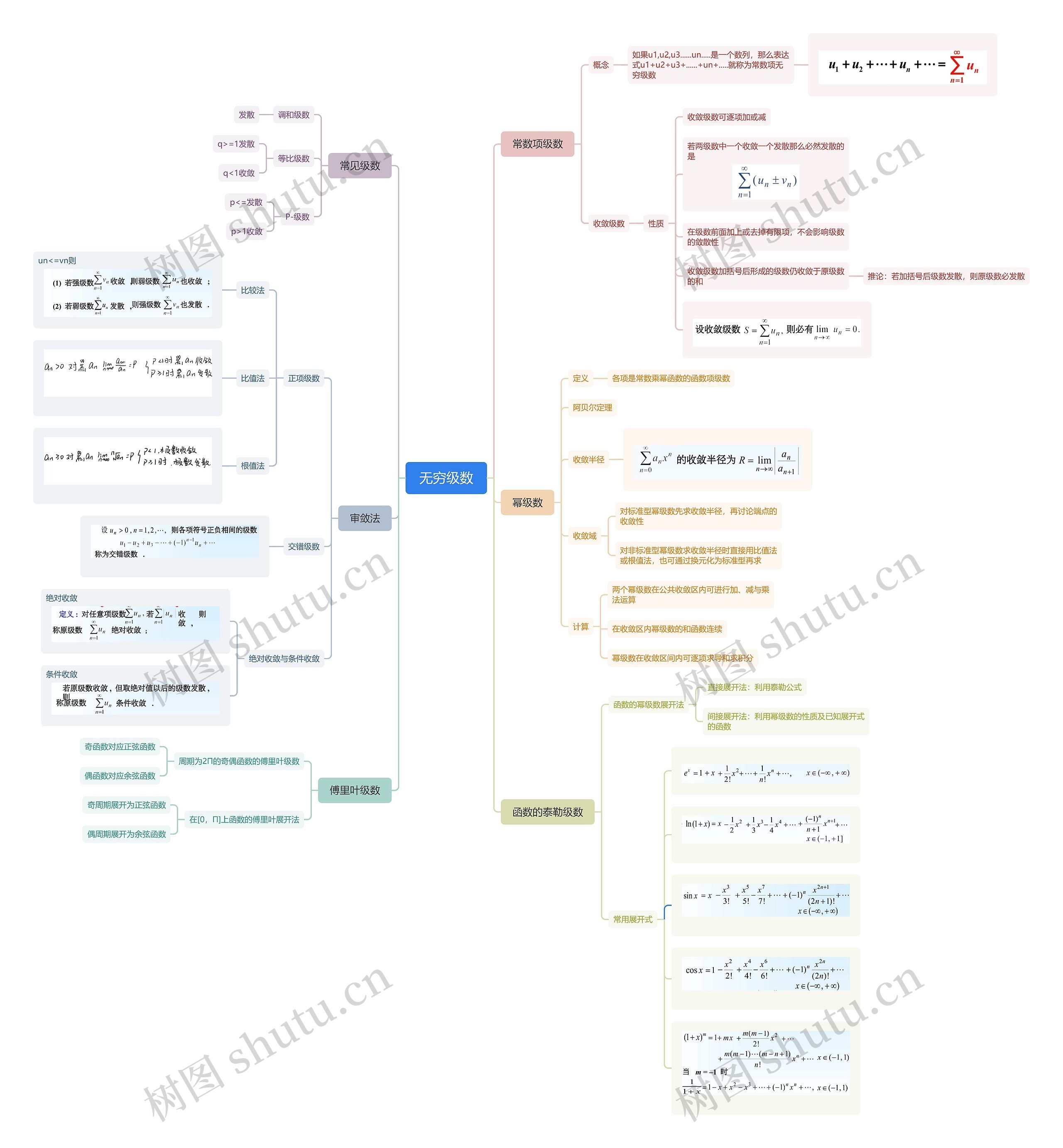
高等数学无穷级数相关内容知识讲解
树图思维导图提供 无穷级数思维脑图 在线思维导图免费制作，点击“编辑”按钮，可对 无穷级数思维脑图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：42c6bcbae6e0a541efd7ed3aca22bf83
思维导图大纲
无穷级数思维导图模板大纲
常数项级数
概念
如果u1,u2,u3......un.....是一个数列，那么表达式u1+u2+u3+......+un+.....就称为常数项无穷级数
收敛级数
性质
收敛级数可逐项加或减
若两级数中一个收敛一个发散那么必然发散的是
在级数前面加上或去掉有限项，不会影响级数的敛散性
收敛级数加括号后形成的级数仍收敛于原级数的和
推论：若加括号后级数发散，则原级数必发散
常见级数
调和级数
发散
等比级数
q>=1发散
q<1收敛
P-级数
p<=发散
p>1收敛
审敛法
正项级数
比较法
un<=vn则
比值法
根值法
交错级数
绝对收敛与条件收敛
绝对收敛
条件收敛
幂级数
定义
各项是常数乘幂函数的函数项级数
阿贝尔定理
收敛半径
收敛域
对标准型幂级数先求收敛半径，再讨论端点的收敛性
对非标准型幂级数求收敛半径时直接用比值法或根值法，也可通过换元化为标准型再求
计算
两个幂级数在公共收敛区内可进行加、减与乘法运算
在收敛区内幂级数的和函数连续
幂级数在收敛区间内可逐项求导和求积分
函数的泰勒级数
函数的幂级数展开法
直接展开法：利用泰勒公式
间接展开法：利用幂级数的性质及已知展开式的函数
常用展开式
傅里叶级数
周期为2Π的奇偶函数的傅里叶级数
奇函数对应正弦函数
偶函数对应余弦函数
在[0，Π]上函数的傅里叶展开法
奇周期展开为正弦函数
偶周期展开为余弦函数
相关思维导图模板
树图思维导图提供 1107文家市玉萍思维导图 在线思维导图免费制作，点击“编辑”按钮，可对 1107文家市玉萍思维导图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：ed943ef641f6dc874860eb6095857ed6
树图思维导图提供 种子思维脑图 在线思维导图免费制作，点击“编辑”按钮，可对 种子思维脑图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：86f8307a40ea24607c6c79354e09377f
沪公网安备 31011502019485号
上海工商