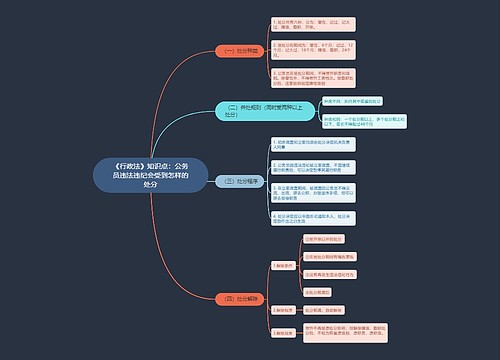
行测数量关系之交替完工有妙招思维导图
工程问题中的交替完工问题在行测数量关系中属于难度偏高的题目,很多考生在做这一类题型时,由于不够熟练,没有掌握到做题的方法导致做起来比较费时间。今天我们就来学习一下这类题型。
树图思维导图提供 行测数量关系之交替完工有妙招 在线思维导图免费制作,点击“编辑”按钮,可对 行测数量关系之交替完工有妙招 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0887c21841280b46161a8df602c7fac2
思维导图大纲
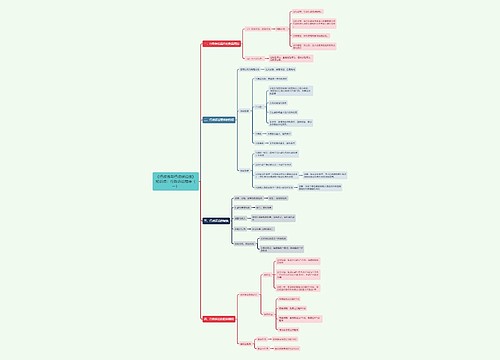
行测数量关系:交替完工有妙招思维导图模板大纲
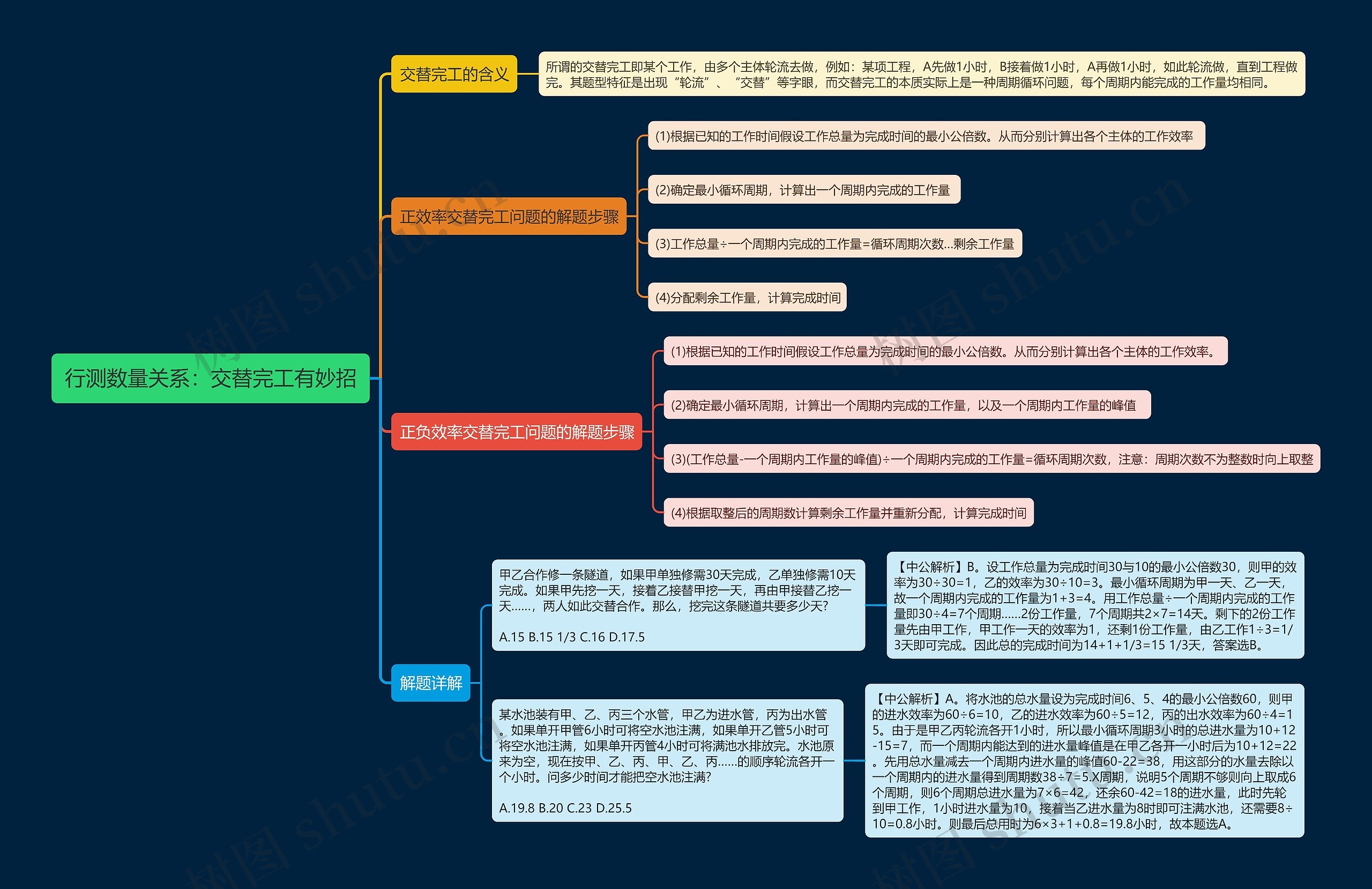
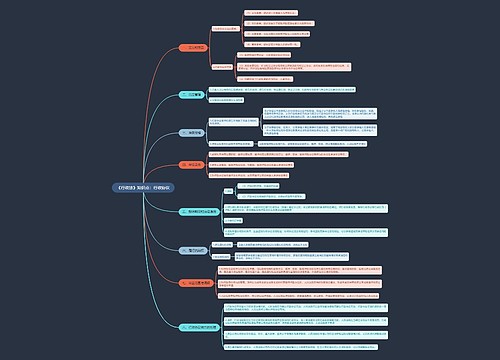
交替完工的含义
所谓的交替完工即某个工作,由多个主体轮流去做,例如:某项工程,A先做1小时,B接着做1小时,A再做1小时,如此轮流做,直到工程做完。其题型特征是出现“轮流”、“交替”等字眼,而交替完工的本质实际上是一种周期循环问题,每个周期内能完成的工作量均相同。
正效率交替完工问题的解题步骤
(1)根据已知的工作时间假设工作总量为完成时间的最小公倍数。从而分别计算出各个主体的工作效率
(2)确定最小循环周期,计算出一个周期内完成的工作量
(3)工作总量÷一个周期内完成的工作量=循环周期次数…剩余工作量
(4)分配剩余工作量,计算完成时间
正负效率交替完工问题的解题步骤
(1)根据已知的工作时间假设工作总量为完成时间的最小公倍数。从而分别计算出各个主体的工作效率。
(2)确定最小循环周期,计算出一个周期内完成的工作量,以及一个周期内工作量的峰值
(3)(工作总量-一个周期内工作量的峰值)÷一个周期内完成的工作量=循环周期次数,注意:周期次数不为整数时向上取整
(4)根据取整后的周期数计算剩余工作量并重新分配,计算完成时间
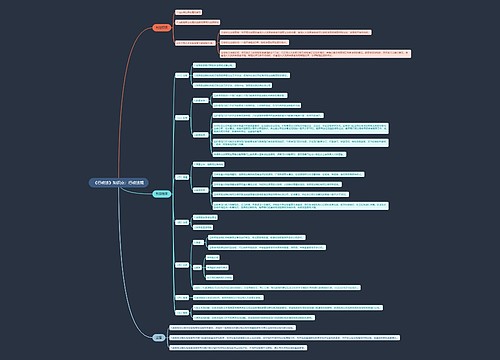
解题详解
甲乙合作修一条隧道,如果甲单独修需30天完成,乙单独修需10天完成。如果甲先挖一天,接着乙接替甲挖一天,再由甲接替乙挖一天……,两人如此交替合作。那么,挖完这条隧道共要多少天? A.15 B.15 1/3 C.16 D.17.5
【中公解析】B。设工作总量为完成时间30与10的最小公倍数30,则甲的效率为30÷30=1,乙的效率为30÷10=3。最小循环周期为甲一天、乙一天,故一个周期内完成的工作量为1+3=4。用工作总量÷一个周期内完成的工作量即30÷4=7个周期……2份工作量,7个周期共2×7=14天。剩下的2份工作量先由甲工作,甲工作一天的效率为1,还剩1份工作量,由乙工作1÷3=1/3天即可完成。因此总的完成时间为14+1+1/3=15 1/3天,答案选B。
某水池装有甲、乙、丙三个水管,甲乙为进水管,丙为出水管。如果单开甲管6小时可将空水池注满,如果单开乙管5小时可将空水池注满,如果单开丙管4小时可将满池水排放完。水池原来为空,现在按甲、乙、丙、甲、乙、丙……的顺序轮流各开一个小时。问多少时间才能把空水池注满? A.19.8 B.20 C.23 D.25.5
【中公解析】A。将水池的总水量设为完成时间6、5、4的最小公倍数60,则甲的进水效率为60÷6=10,乙的进水效率为60÷5=12,丙的出水效率为60÷4=15。由于是甲乙丙轮流各开1小时,所以最小循环周期3小时的总进水量为10+12-15=7,而一个周期内能达到的进水量峰值是在甲乙各开一小时后为10+12=22。先用总水量减去一个周期内进水量的峰值60-22=38,用这部分的水量去除以一个周期内的进水量得到周期数38÷7=5.X周期,说明5个周期不够则向上取成6个周期,则6个周期总进水量为7×6=42,还余60-42=18的进水量,此时先轮到甲工作,1小时进水量为10,接着当乙进水量为8时即可注满水池,还需要8÷10=0.8小时。则最后总用时为6×3+1+0.8=19.8小时,故本题选A。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 埃隆·马斯克的商业版图 在线思维导图免费制作,点击“编辑”按钮,可对 埃隆·马斯克的商业版图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7464362ac911e8a334867bb3fc7a2346





 上海工商
上海工商