公务员行测复习等差数列求和公式思维导图

查看详情

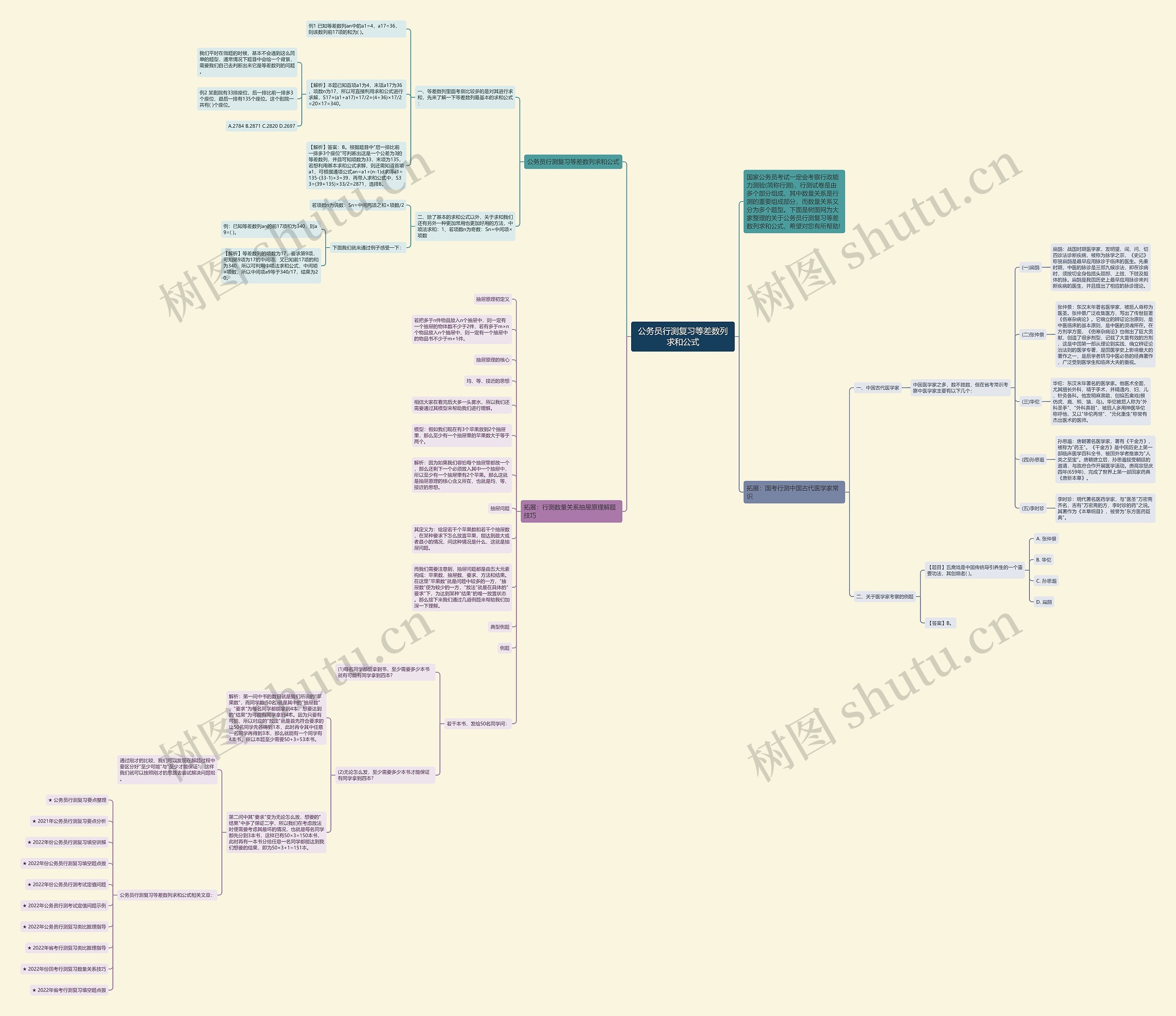
国家公务员考试一定会考察行政能力测验(简称行测)，行测试卷是由多个部分组成，其中数量关系是行测的重要组成部分，而数量关系又分为多个题型。

树图思维导图提供公务员行测复习等差数列求和公式在线思维导图免费制作，点击“编辑”按钮，可对公务员行测复习等差数列求和公式进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：362bc7c98a2b0f8a2f2fd87711b299f3

行测等差数列公式公务员行测复习公务员行测复习

举报/反馈

思维导图大纲

公务员行测复习等差数列求和公式思维导图模板大纲

国家公务员考试一定会考察行政能力测验(简称行测)，行测试卷是由多个部分组成，其中数量关系是行测的重要组成部分，而数量关系又分为多个题型。下面是树图网为大家整理的关于公务员行测复习等差数列求和公式，希望对您有所帮助!

公务员行测复习等差数列求和公式

一、等差数列里面考察比较多的是对其进行求和，先来了解一下等差数列最基本的求和公式：

例1 已知等差数列an中的a1=4，a17=36，则该数列前17项的和为( )。

【解析】本题已知首项a1为4，末项a17为36，项数n为17，所以可直接利用求和公式进行求解，S17=(a1+a17)×17/2=(4+36)×17/2=20×17=340。

我们平时在做题的时候，基本不会遇到这么简单的题型，通常情况下题目中会给一个背景，需要我们自己去判断出来它是等差数列的问题。

例2 某剧院有33排座位，后一排比前一排多3个座位，最后一排有135个座位。这个剧院一共有( )个座位。

A.2784 B.2871 C.2820 D.2697

【解析】答案：B。根据题目中"后一排比前一排多3个座位"可判断出这是一个公差为3的等差数列，并且可知项数为33，末项为135，若想利用基本求和公式求解，则还需知道首项a1，可根据通项公式an=a1+(n-1)d求得a1=135-(33-1)×3=39，再带入求和公式中，S33=(39+135)×33/2=2871，选择B。

二、除了基本的求和公式以外，关于求和我们还有另外一种更加常用也更加好用的方法，中项法求和：1、若项数n为奇数：Sn=中间项×项数

若项数n为偶数：Sn=中间两项之和×项数/2

下面我们就来通过例子感受一下：

例：已知等差数列an的前17项和为340，则a9=( )。

【解析】等差数列的项数为17，要求第9项，可知第9项为17的中间项，又已知前17项的和为340，所以可利用中项法求和公式，中间项×项数，所以中间项a9等于340/17，结果为20。

拓展：国考行测中国古代医学家常识

一、中国古代医学家

中国医学家之多，数不胜数，但在省考常识考察中医学家主要有以下几个：

(一)扁鹊

扁鹊：战国时期医学家，发明望、闻、问、切四诊法诊断疾病，被称为脉学之宗，《史记》称赞扁鹊是最早应用脉诊于临床的医生。先秦时期，中医的脉诊是三部九候诊法，即在诊病时，须按切全身包括头颈部、上肢、下肢及躯体的脉。扁鹊是我国历史上最早应用脉诊来判断疾病的医生，并且提出了相应的脉诊理论。

(二)张仲景

张仲景：东汉末年著名医学家，被后人尊称为医圣。张仲景广泛收集医方，写出了传世巨著《伤寒杂病论》。它确立的辨证论治原则，是中医临床的基本原则，是中医的灵魂所在。在方剂学方面，《伤寒杂病论》也做出了巨大贡献，创造了很多剂型，记载了大量有效的方剂，这是中国第一部从理论到实践、确立辨证论治法则的医学专著，是国医学史上影响最大的著作之一，是后学者研习中医必备的经典著作，广泛受到医学生和临床大夫的重视。

(三)华佗

华佗：东汉末年著名的医学家。他医术全面，尤其擅长外科，精于手术，并精通内、妇、儿、针灸各科。他发明麻沸散，创编五禽戏(模仿虎、鹿、熊、猿、鸟)。华佗被后人称为"外科圣手"、"外科鼻祖"，被后人多用神医华佗称呼他，又以"华佗再世"、"元化重生"称誉有杰出医术的医师。

(四)孙思邈

孙思邈：唐朝著名医学家，著有《千金方》，被称为"药王"。《千金方》是中国历史上第一部临床医学百科全书，被国外学者推崇为"人类之至宝"。唐朝建立后，孙思邈接受朝廷的邀请，与政府合作开展医学活动。唐高宗显庆四年(659年)，完成了世界上第一部国家药典《唐新本草》。

(五)李时珍

李时珍：明代著名医药学家，与"医圣"万密斋齐名，古有"万密斋的方，李时珍的药"之说。其著作为《本草纲目》，被誉为"东方医药巨典"。

二、关于医学家考察的例题

【题目】五禽戏是中国传统导引养生的一个重要功法，其创编者( )。

A. 张仲景

B. 华佗

C. 孙思邈

D. 扁鹊

【答案】B。

拓展：行测数量关系抽屉原理解题技巧

抽屉原理初定义

若把多于n件物品放入n个抽屉中，则一定有一个抽屉的物体数不少于2件，若有多于m×n个物品放入n个抽屉中，则一定有一个抽屉中的物品书不少于m+1件。

抽屉原理的核心

均、等、接近的思想

相信大家在看完后大多一头雾水，所以我们还需要通过其模型来帮助我们进行理解。

模型：假如我们现在有3个苹果放到2个抽屉里，那么至少有一个抽屉里的苹果数大于等于两个。

解析：因为如果我们哪怕每个抽屉里都放一个，那么还剩下一个必须放入其中一个抽屉中，所以至少有一个抽屉里有2个苹果。那么这就是抽屉原理的核心含义所在，也就是均、等、接近的思想。

抽屉问题

其定义为：给定若干个苹果数和若干个抽屉数，在某种要求下怎么放置苹果，能达到最大或者最小的情况，问这种情况是什么，这就是抽屉问题。

而我们需要注意到，抽屉问题都是由五大元素构成：苹果数、抽屉数、要求、方法和结果。在这里"苹果数"就是问题中较多的一方，"抽屉数"便为较少的一方，"放法"就是在具体的"要求"下，为达到某种"结果"的唯一放置状态。那么接下来我们通过几道例题来帮助我们加深一下理解。

典型例题

例题

若干本书，发给50名同学问：

(1)每名同学都能拿到书，至少需要多少本书就有可能有同学拿到四本?

(2)无论怎么发，至少需要多少本书才能保证有同学拿到四本?

解析：第一问中书的数目就是我们所说的"苹果数"，而同学数(50名)就是其中的"抽屉数"，"要求"为每名同学都能拿到4本，想要达到的"结果"为可能有同学拿到4本。因为只要有可能，所以对应的"放法"就是首先符合要求的让50名同学先各得到1本，此时再令其中任意一名同学再得到3本，那么就能有一个同学有4本书。所以本题至少需要50+3=53本书。

第二问中其"要求"变为无论怎么放，想要的"结果"中多了保证二字，所以我们在考虑放法时便需要考虑其最坏的情况，也就是每名同学都先分到3本书，这样已有50×3=150本书，此时再有一本书分给任意一名同学都能达到我们想要的结果，即为50×3+1=151本。

通过刚才的比较，我们可以发现在解题过程中要区分好"至少可能"与"至少才能保证"，这样我们就可以按照刚才的思路去尝试解决问题啦。

公务员行测复习等差数列求和公式相关文章：

★ 公务员行测复习要点整理

★ 2021年公务员行测复习要点分析

★ 2022年份公务员行测复习填空讲解

★ 2022年份公务员行测复习填空题点拨

★ 2022年份公务员行测考试定值问题

★ 2022年公务员行测考试定值问题示例

★ 2022年公务员行测复习类比推理指导

★ 2022年省考行测复习类比推理指导

★ 2022年份国考行测复习数量关系技巧