什么是无理数 无理数的概念|中学数学思维导图

什么是无理数无理数的概念|中学数学思维导图,无理数就是所有不是有理数字的实数,他不能写作两个整数之比,小数点之后的数字有无限多个,不会循环。无理数的另一特征是无限的连分数表达式,是无限不循环小数,常见的无理数有非完全平方数的平方根、π和e(其中后两者均为超越数)。无理数具有许多性质,如无理数加(减)无理数既可以是无理数又可以是有理数,无理数乘(除)无理数既可以是无理数又可以是有理数,无理数加(减)有理数一定是无理数,无理数乘(除)一个非0有理数一定是无理数。
思维导图大纲
什么是无理数 无理数的概念|中学数学思维导图模板大纲
无理数,也称为无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。 常见的无理数有非完全平方数的平方根、π和e(其中后两者均为超越数)等。无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。
数学中,无理数是所有不是有理数字的实数,后者是由整数的比率(或分数)构成的数字。当两个线段的长度比是无理数时,线段也被描述为不可比较的,这意味着它们不能"测量",即没有长度("度量")。
常见的无理数有:圆周长与其直径的比值,欧拉数e,黄金比例φ等等。
即非有理数之实数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。常见的无理数有大部分的平方根、π和e(其中后两者同时为超越数)等。无理数是无限不循环小数。如圆周率π等。
无理数性质
无限不循环的小数就是无理数 。换句话说,就是不可以化为整数或者整数比的数
性质1 无理数加(减)无理数既可以是无理数又可以是有理数
性质2 无理数乘(除)无理数既可以是无理数又可以是有理数
性质3 无理数加(减)有理数一定是无理数
性质4 无理数乘(除)一个非0有理数一定是无理数
相关思维导图模板


树图思维导图提供 初中数学优秀的教学设计 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学优秀的教学设计 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6ce8b8fd75ac89af8b656c7dc82aa5db
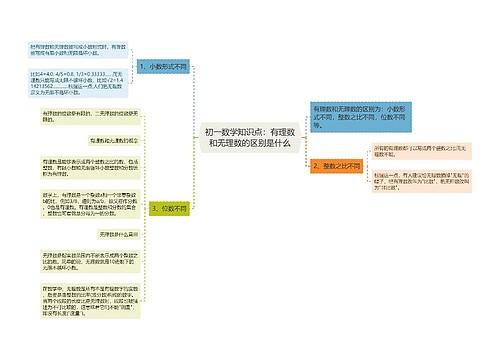

树图思维导图提供 初一数学知识点:有理数和无理数的区别是什么 在线思维导图免费制作,点击“编辑”按钮,可对 初一数学知识点:有理数和无理数的区别是什么 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:354d2d7b10089e185dbba1b5d79713f1









 上海工商
上海工商