2022九年级数学关于有理数概念总结思维导图
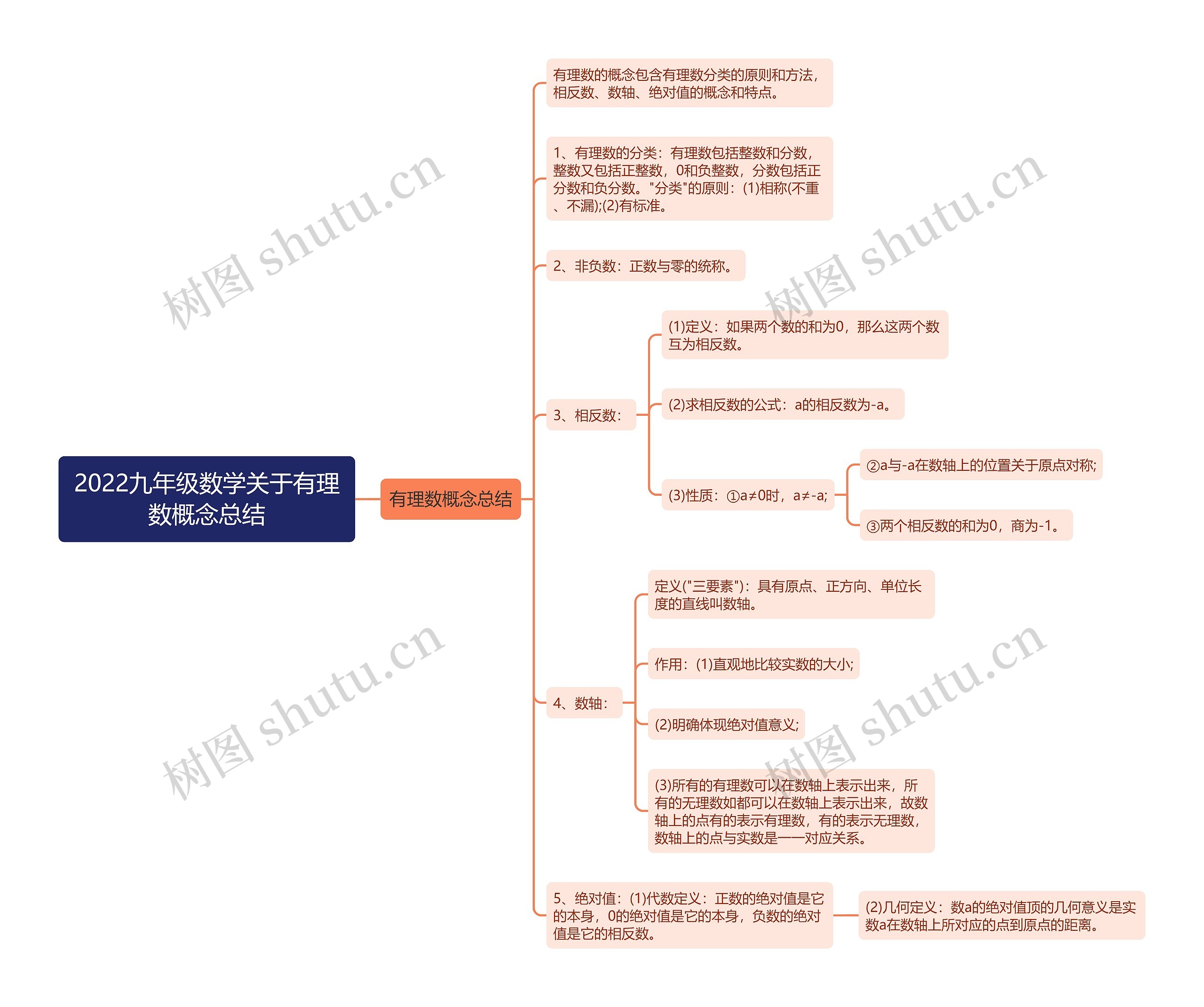
2022九年级数学关于有理数概念总结思维导图，包含了有理数的分类原则和方法，相反数、数轴、和绝对值的概念和特点，有理数包含整数和分数，而整数包含正整数、0和负整数，分数包含正分数和负分数，这些数的分类原则在有称和标准的基础上进行，非负数是指正数和零的总称，而相反数是指在数轴上相对位置对称的两个数字。数轴作为一个具有原点、正方向和单位长度的直线，可以直观比较实数大小和明确绝对值的意义，绝对值则有代数定义和几何定义，分别表示为正数本身、0本身和负数相反数，在数轴上的表示为实数a数轴上所对应的点到原点的距离。
思维导图大纲
2022九年级数学关于有理数概念总结思维导图模板大纲
有理数概念总结
有理数的概念包含有理数分类的原则和方法，相反数、数轴、绝对值的概念和特点。
1、有理数的分类：有理数包括整数和分数，整数又包括正整数，0和负整数，分数包括正分数和负分数。"分类"的原则：(1)相称(不重、不漏);(2)有标准。
2、非负数：正数与零的统称。
3、相反数：
(1)定义：如果两个数的和为0，那么这两个数互为相反数。
(2)求相反数的公式：a的相反数为-a。
(3)性质：①a≠0时，a≠-a;
②a与-a在数轴上的位置关于原点对称;
③两个相反数的和为0，商为-1。
4、数轴：
定义("三要素")：具有原点、正方向、单位长度的直线叫数轴。
作用：(1)直观地比较实数的大小;
(2)明确体现绝对值意义;
(3)所有的有理数可以在数轴上表示出来，所有的无理数如都可以在数轴上表示出来，故数轴上的点有的表示有理数，有的表示无理数，数轴上的点与实数是一一对应关系。
5、绝对值：(1)代数定义：正数的绝对值是它的本身，0的绝对值是它的本身，负数的绝对值是它的相反数。
(2)几何定义：数a的绝对值顶的几何意义是实数a在数轴上所对应的点到原点的距离。
相关思维导图模板
树图思维导图提供 2022七年级数学下册教学计划（20篇） 在线思维导图免费制作，点击“编辑”按钮，可对 2022七年级数学下册教学计划（20篇） 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：f77b7c6e3985fc44d5046c8aef8255a5
沪公网安备 31011502019485号
上海工商