高二数学期中复习题(第一学年)思维导图
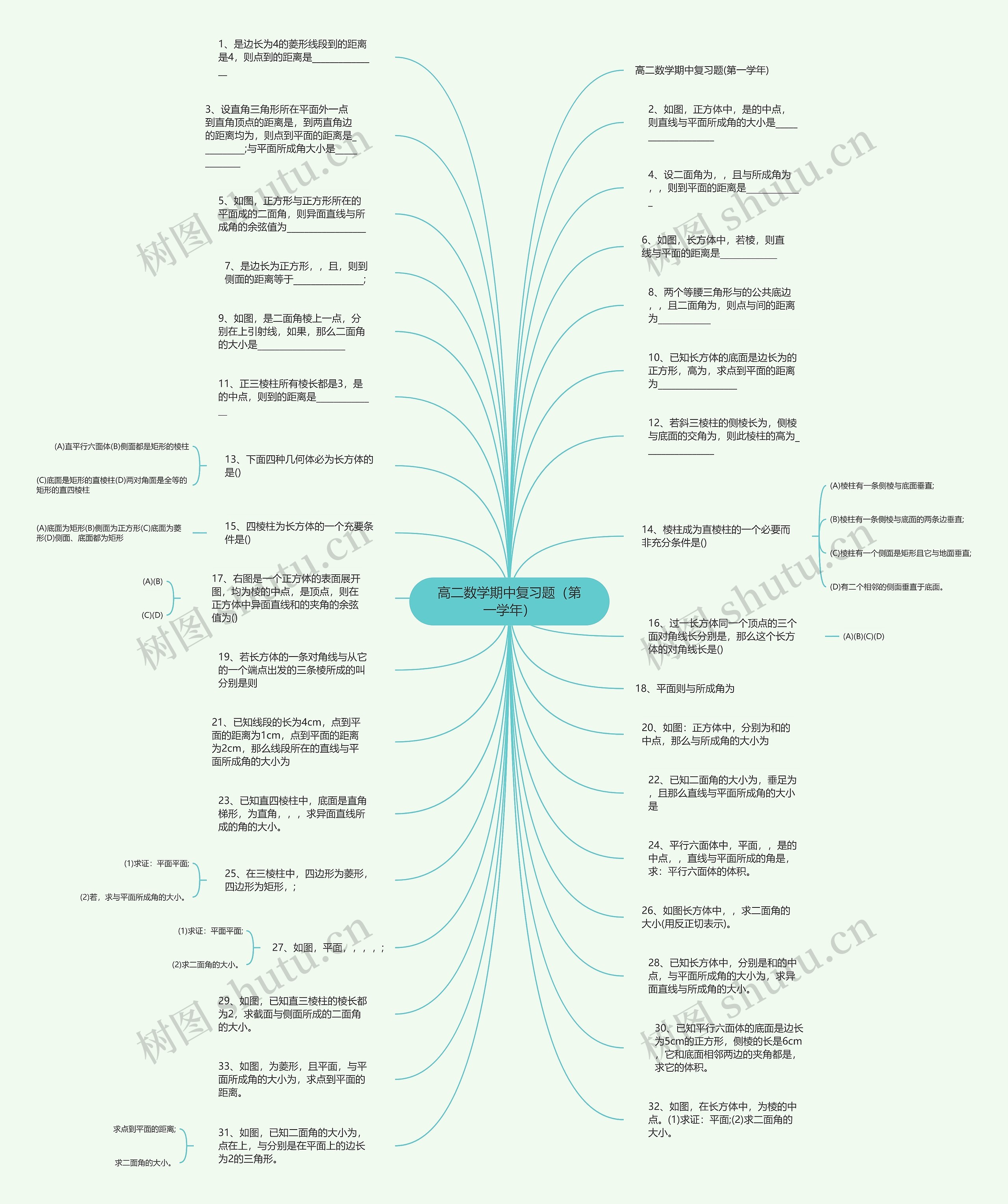
高二数学期中复习题(第一学年)思维导图包含以下知识点:1.点到线段的距离公式,
2.两个正方体表面相交的直线与平面所成角的计算,
3.点到直角三角形平面的距离和与平面所成角的计算,
4.二面角与平面距离的关系,
5.正方形与平面成的二面角与异面直线的夹角,
6.长方体中直线与平面的距离计算,
7.点到正方形侧面的距离计算,
8.等腰三角形与二面角所成角的计算,
9.二面角大小的计算,
10.点到长方体平面的距离计算,
11.正三棱柱中点到顶点的距离计算,
12.斜三棱柱/的高的计算,
13.长方体和其他几何体的对比,长方体的特征,
14.直棱柱的条件,
15.长方体和四棱柱的条件,
16.长方体对角线的计算,
17.正方体的异面直线与角的计算,
18.平面与直线所成角的计算,
19.长方体对角线与棱的关系,
20.正方体中线与角的计算,
21.点到平面的距离和线段所在直线与平面所成角的计算,
22.二面角和直线与平面所成角的计算,
23.直四棱柱中异面直线所成角的计算。
这些知识点涵盖了高二数学中的几何题型和计算方法,能够帮助学生复习期中考试的相关内容。
思维导图大纲
高二数学期中复习题(第一学年)思维导图模板大纲
高二数学期中复习题(第一学年)
1、是边长为4的菱形线段到的距离是4,则点到的距离是_______________
2、如图,正方体中,是的中点,则直线与平面所成角的大小是____________________
3、设直角三角形所在平面外一点到直角顶点的距离是,到两直角边的距离均为,则点到平面的距离是__________;与平面所成角大小是_____________
4、设二面角为,,且与所成角为,,则到平面的距离是_____________
5、如图,正方形与正方形所在的平面成的二面角,则异面直线与所成角的余弦值为__________________
6、如图,长方体中,若棱,则直线与平面的距离是_____________
7、是边长为正方形,,且,则到侧面的距离等于________________;
8、两个等腰三角形与的公共底边,,且二面角为,则点与间的距离为____________
9、如图,是二面角棱上一点,分别在上引射线,如果,那么二面角的大小是____________________
10、已知长方体的底面是边长为的正方形,高为,求点到平面的距离为__________________
11、正三棱柱所有棱长都是3,是的中点,则到的距离是______________
12、若斜三棱柱的侧棱长为,侧棱与底面的交角为,则此棱柱的高为________________
13、下面四种几何体必为长方体的是()
(A)直平行六面体(B)侧面都是矩形的棱柱
(C)底面是矩形的直棱柱(D)两对角面是全等的矩形的直四棱柱
14、棱柱成为直棱柱的一个必要而非充分条件是()
(A)棱柱有一条侧棱与底面垂直;
(B)棱柱有一条侧棱与底面的两条边垂直;
(C)棱柱有一个侧面是矩形且它与地面垂直;
(D)有二个相邻的侧面垂直于底面。
15、四棱柱为长方体的一个充要条件是()
(A)底面为矩形(B)侧面为正方形(C)底面为菱形(D)侧面、底面都为矩形
16、过一长方体同一个顶点的三个面对角线长分别是,那么这个长方体的对角线长是()
(A)(B)(C)(D)
17、右图是一个正方体的表面展开图,均为棱的中点,是顶点,则在正方体中异面直线和的夹角的余弦值为()
(A)(B)
(C)(D)
18、平面则与所成角为
19、若长方体的一条对角线与从它的一个端点出发的三条棱所成的叫分别是则
20、如图:正方体中,分别为和的中点,那么与所成角的大小为
21、已知线段的长为4cm,点到平面的距离为1cm,点到平面的距离为2cm,那么线段所在的直线与平面所成角的大小为
22、已知二面角的大小为,垂足为,且那么直线与平面所成角的大小是
23、已知直四棱柱中,底面是直角梯形,为直角,,,求异面直线所成的角的大小。
24、平行六面体中,平面,,是的中点,,直线与平面所成的角是,求:平行六面体的体积。
25、在三棱柱中,四边形为菱形,四边形为矩形,;
(1)求证:平面平面;
(2)若,求与平面所成角的大小。
26、如图长方体中,,求二面角的大小(用反正切表示)。
27、如图,平面,,,,;
(1)求证:平面平面;
(2)求二面角的大小。
28、已知长方体中,分别是和的中点,与平面所成角的大小为,求异面直线与所成角的大小。
29、如图,已知直三棱柱的棱长都为2,求截面与侧面所成的二面角的大小。
30、已知平行六面体的底面是边长为5cm的正方形,侧棱的长是6cm,它和底面相邻两边的夹角都是,求它的体积。
33、如图,为菱形,且平面,与平面所成角的大小为,求点到平面的距离。
32、如图,在长方体中,为棱的中点。(1)求证:平面;(2)求二面角的大小。
31、如图,已知二面角的大小为,点在上,与分别是在平面上的边长为2的三角形。
求点到平面的距离;
求二面角的大小。
相关思维导图模板


树图思维导图提供 2021数学科目教学心得总结 在线思维导图免费制作,点击“编辑”按钮,可对 2021数学科目教学心得总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:8e6a749fca08f37ca7b9b0b5d17df941









 上海工商
上海工商