高二数学备考:判断充分与必要条件的常用方法思维导图
高二数学备考:判断充分与必要条件的常用方法思维导图模板大纲,判断充分条件与必要条件是高中阶段非常重要的数学概念。他涉及的知识范围广泛,综合性强,能与高中任何知识相结合,有一定的深度和难度,解决此类问题需要我们掌握以下知识点。
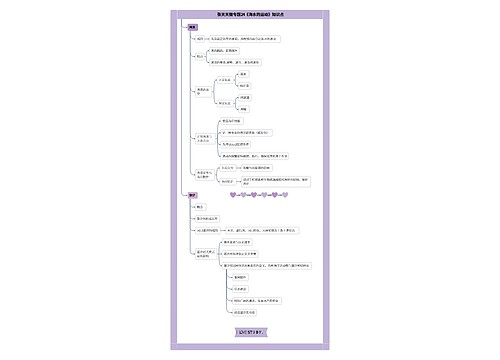
一、定义法
在解答此类题目时,可以利用定义直接推导。需要抓住命题的条件和结论的四种关系的定义,已知条件p确定了m,n的范围,结论q明确了方程的根的特点,可以联想到根与系数的关系,进一步化简。通过推导可以判断p是否是q的条件。
二、集合法
将命题p和q分别看作两个集合A和B,用集合意识解释条件。根据集合的关系,可以得出以下结论:
1.若A包含于B,则x∈A是x∈B的充分条件,x∈B是x∈A的必要条件。
2.若A不完全包含于B,则x∈A是x∈B的充分不必要条件,x∈B是x∈A的必要不充分条件。
3.若A与B相等,则x∈A和x∈B互为充要条件。
4.若A与B既不完全包含于对方,也不相等,则x∈A和x∈B互为既不充分也不必要条件。
掌握上述方法,能够清晰地判断条件和结论之间的关系,解决判断充分与必要条件的问题,这对于培养学生的逻辑思维能力具有重要意义,在高二数学备考中,需要熟练掌握并灵活运用这些方法。
思维导图大纲
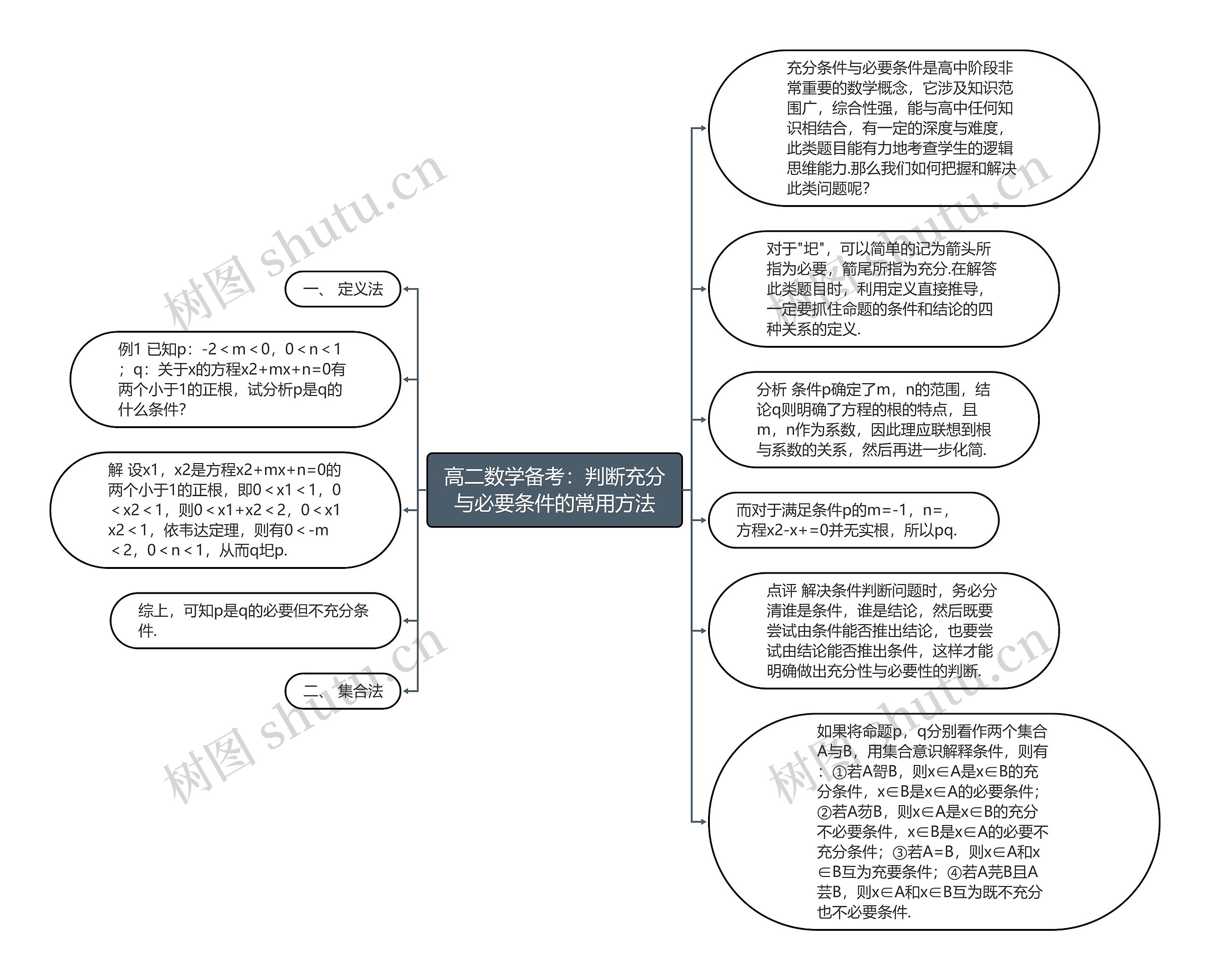
高二数学备考:判断充分与必要条件的常用方法思维导图模板大纲
充分条件与必要条件是高中阶段非常重要的数学概念,它涉及知识范围广,综合性强,能与高中任何知识相结合,有一定的深度与难度,此类题目能有力地考查学生的逻辑思维能力.那么我们如何把握和解决此类问题呢?
一、 定义法
对于"圯",可以简单的记为箭头所指为必要,箭尾所指为充分.在解答此类题目时,利用定义直接推导,一定要抓住命题的条件和结论的四种关系的定义.
例1 已知p:-2<m<0,0<n<1;q:关于x的方程x2+mx+n=0有两个小于1的正根,试分析p是q的什么条件?
分析 条件p确定了m,n的范围,结论q则明确了方程的根的特点,且m,n作为系数,因此理应联想到根与系数的关系,然后再进一步化简.
解 设x1,x2是方程x2+mx+n=0的两个小于1的正根,即0<x1<1,0<x2<1,则0<x1+x2<2,0<x1x2<1,依韦达定理,则有0<-m<2,0<n<1,从而q圯p.
而对于满足条件p的m=-1,n=,方程x2-x+=0并无实根,所以pq.
综上,可知p是q的必要但不充分条件.
点评 解决条件判断问题时,务必分清谁是条件,谁是结论,然后既要尝试由条件能否推出结论,也要尝试由结论能否推出条件,这样才能明确做出充分性与必要性的判断.
二、 集合法
如果将命题p,q分别看作两个集合A与B,用集合意识解释条件,则有:①若A哿B,则x∈A是x∈B的充分条件,x∈B是x∈A的必要条件;②若A芴B,则x∈A是x∈B的充分不必要条件,x∈B是x∈A的必要不充分条件;③若A=B,则x∈A和x∈B互为充要条件;④若A芫B且A芸B,则x∈A和x∈B互为既不充分也不必要条件.
相关思维导图模板


树图思维导图提供 数学高二文科教学总结 在线思维导图免费制作,点击“编辑”按钮,可对 数学高二文科教学总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f7d48f2bc6a62c717139a53d3b535197











 上海工商
上海工商