高二数学备考:数学解析几何中求参数取值范围的方法三思维导图
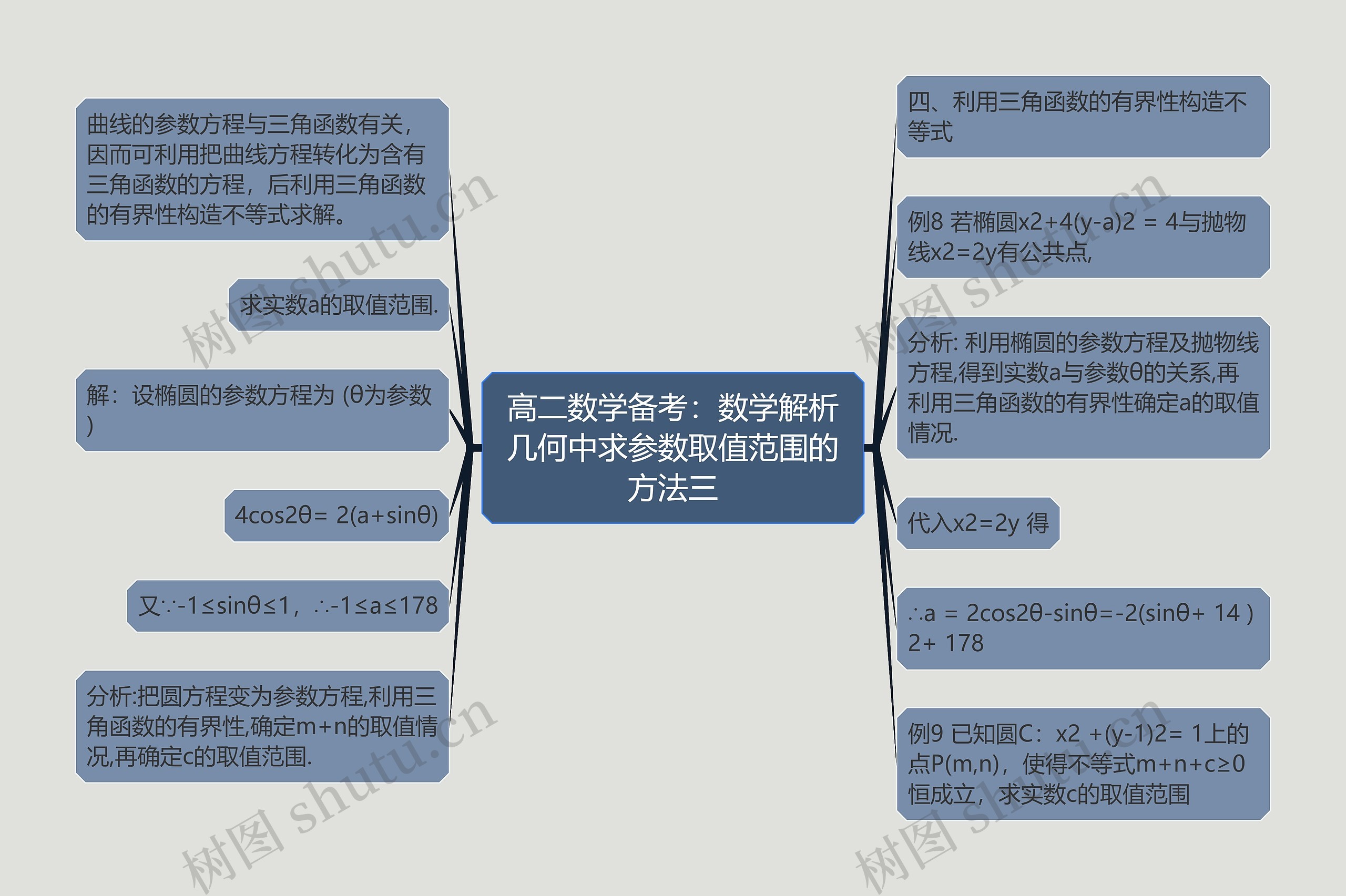
高二数学备考:数学解析几何中求参数取值范围的方法三思维导图可以帮助我们解决一些包含曲线参数方程和三角函数的问题,我们可以利用椭圆和抛物线的参数方程来推导实数a和参数θ的关系,利用三角函数的有界性来确定a的取值范围。举例来说,如果给定椭圆x2+4(y-a)2=4与抛物线x2=2y有公共点的条件,可以通过将参数方程代入抛物线方程得到一个含有三角函数的方程,再利用三角函数的有界性来确定实数a的取值范围。同理,对于给定圆C:x2+(y-1)2=1上的点P(m,n),使得不等式m+n+c≥0恒成立的条件,可以将圆的方程转化为参数方程,并利用三角函数的有界性来确定m+n的取值范围,最后在确定实数c的取值范围,通过这种思维导图的方法,可以更清晰地理解和解决这类问题。
思维导图大纲
高二数学备考:数学解析几何中求参数取值范围的方法三思维导图模板大纲
四、利用三角函数的有界性构造不等式
曲线的参数方程与三角函数有关,因而可利用把曲线方程转化为含有三角函数的方程,后利用三角函数的有界性构造不等式求解。
例8 若椭圆x2+4(y-a)2 = 4与抛物线x2=2y有公共点,
求实数a的取值范围.
分析: 利用椭圆的参数方程及抛物线方程,得到实数a与参数θ的关系,再利用三角函数的有界性确定a的取值情况.
解:设椭圆的参数方程为 (θ为参数)
代入x2=2y 得
4cos2θ= 2(a+sinθ)
∴a = 2cos2θ-sinθ=-2(sinθ+ 14 )2+ 178
又∵-1≤sinθ≤1,∴-1≤a≤178
例9 已知圆C:x2 +(y-1)2= 1上的点P(m,n),使得不等式m+n+c≥0恒成立,求实数c的取值范围
分析:把圆方程变为参数方程,利用三角函数的有界性,确定m+n的取值情况,再确定c的取值范围.
相关思维导图模板

树图思维导图提供 高考数学知识点实用 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学知识点实用 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f2e0583b31071d22a8fd080d40e0b9b8

树图思维导图提供 2023高考数学知识点 在线思维导图免费制作,点击“编辑”按钮,可对 2023高考数学知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:67e43c5f03e398f10383430b79cdeb20

















 上海工商
上海工商