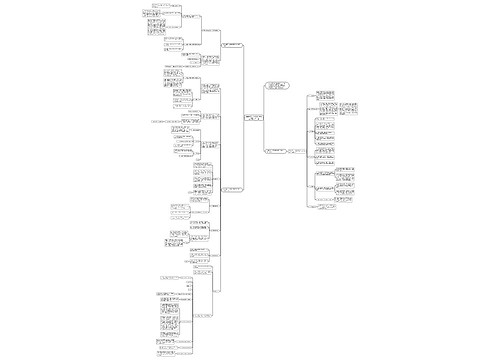
2018高考数学答题方法:函数与导数解题技巧思维导图

2018高考数学答题方法:函数与导数解题技巧思维导图重点是基本初等函数和函数的相关概念和运算,思维导图模板提到利用导数研究函数性质,在复习中应以三次函数的图象形状特征为主线,探索函数的单调性、极值、零点,求切线方程的导数的几何意义及解题方法,思维导图模板指出求函数的单调区间实际上就是解导数不等式的过程,排列函数单调区间需要正确分区并确定边界。分类与整合思想在函数与导数的求解问题中也是必考的方法,思维导图模板提到函数与导数的解答题多放在属于难题且需要说明逻辑严谨性和化归与转化,整篇思维导图模板包含了函数与导数解题的知识点,对于高考复习来说是必备资料,对于高考志愿填报也有必备工具的介绍。
思维导图大纲
2018高考数学答题方法:函数与导数解题技巧思维导图模板大纲
1.客观题的考查往往以 基本初等函数 为载体,全面考查函数概念和基本运算,考查函数的定义域、值域、单调性、奇偶性、对称性、周期性、有界性,以及函数图象变换等核心概念和主干知识,试题属于简单题或中等难度题;
2.利用导数研究函数性质,其研究的过程和方法具有普适性、一般性和有效性,可以迁移到其他函数的研究中。
因此,复习中应以三次函数的图象的形状特征为主线,探索三次函数的单调性、极值、零点个数等问题。
并在此过程中,体会数形结合、分类与整合、化归与转化等思想方法;
3.求切线方程是导数的几何意义的直接应用,审题时尤其要注意「 处 」与「 过 」的区别,
(Ⅰ)点 P ( 0 , -4 ) 在曲线 C 上,曲线 C 在 P ( 0 , -4 )点处的切线的斜率就是在 x = 0 处的导数;
(Ⅱ)曲线 C 过点 P( 0 , -4 ) 的切线不一定以点 P 为切点,解题一般从切点入手,利用切点处的导数是切线的斜率以及切点既在切线上又在曲线上这三个条件,直接或用待定系数法求解切线方程;
4.求函数的单调区间,实际上就是解导数为正或为负的不等式;"求导求驻点,列表看趋势"是求函数单调区间的基本方法,列表之前需要对函数定义域正确分区,其中边界就是 f' ( x ) 的零点。
涉及函数在含参区间的极值问题,可以从含参区间的不同位置入手分类讨论。
分类与整合思想 是必考的思想方法,而且常常落脚于函数与导数,不论是对函数单调性的讨论,还是在研究函数其他性质的求解过程,总是避免不了进行分类讨论。
分类与整合思想是有层次性的,最重要的是,要明白为什么要讨论,以及怎么分类讨论;
5.函数与导数的解答题基本放置于最后一题,属难题。
不论是对某个命题进行讨论还是证明,其解题特点一是强调逻辑的严谨性,二需要化归与转化,而且常常以基本初等函数为载体,利用方程、不等式、数学建模与导数、代数推理等知识点交汇,考查函数五大性质的应用、不等式问题和函数方程思想、数形结合思想、分类讨论思想等。
高考复习必备资料
高考志愿填报必备工具:
相关思维导图模板


树图思维导图提供 2018高考数学答题方法:导数应用解题技巧 在线思维导图免费制作,点击“编辑”按钮,可对 2018高考数学答题方法:导数应用解题技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:8d889a59cd0feafb758f74f12dacfeef

树图思维导图提供 2018高二上学期数学教师上学期工作计划 在线思维导图免费制作,点击“编辑”按钮,可对 2018高二上学期数学教师上学期工作计划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1a40e58211f33a24a18715c4dafa1cb1











 上海工商
上海工商