分治算法:汉诺塔问题思维导图
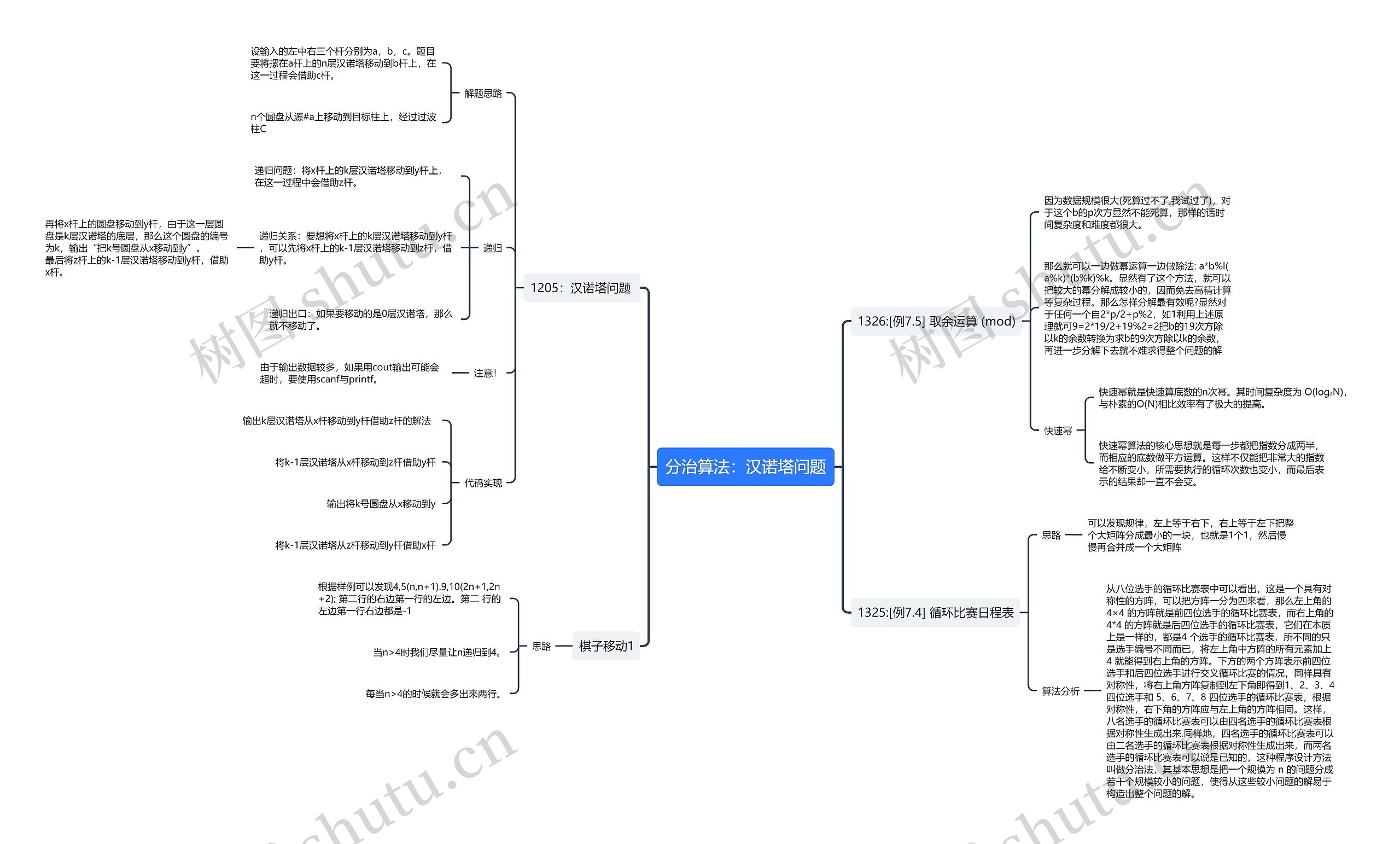
分治算法:汉诺塔问题
树图思维导图提供 分治算法:汉诺塔问题 在线思维导图免费制作,点击“编辑”按钮,可对 分治算法:汉诺塔问题 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:3b3e458ada2786065ddcca9869361230
思维导图大纲
分治算法:汉诺塔问题思维导图模板大纲
1326:[例7.5] 取余运算 (mod)
因为数据规模很大(死算过不了,我试过了),对于这个b的p次方显然不能死算,那样的话时间复杂度和难度都很大。
那么就可以一边做幂运算一边做除法: a*b%l(a%k)*(b%k)%k。显然有了这个方法,就可以把较大的幂分解成较小的,因而免去高精计算等复杂过程。那么怎样分解最有效呢?显然对于任何一个自2*p/2+p%2,如1利用上述原理就可9=2*19/2+19%2=2把b的19次方除以k的余数转换为求b的9次方除以k的余数,再进一步分解下去就不难求得整个问题的解
快速幂
快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高。
快速幂算法的核心思想就是每一步都把指数分成两半,而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。
1205:汉诺塔问题
解题思路
设输入的左中右三个杆分别为a,b,c。题目要将摞在a杆上的n层汉诺塔移动到b杆上,在这一过程会借助c杆。
n个圆盘从源#a上移动到目标柱上,经过过波柱C
递归
递归问题:将x杆上的k层汉诺塔移动到y杆上,在这一过程中会借助z杆。
递归关系:要想将x杆上的k层汉诺塔移动到y杆,可以先将x杆上的k-1层汉诺塔移动到z杆,借助y杆。
再将x杆上的圆盘移动到y杆,由于这一层圆盘是k层汉诺塔的底层,那么这个圆盘的编号为k,输出“把k号圆盘从x移动到y”。 最后将z杆上的k-1层汉诺塔移动到y杆,借助x杆。
递归出口:如果要移动的是0层汉诺塔,那么就不移动了。
注意!
由于输出数据较多,如果用cout输出可能会超时,要使用scanf与printf。
代码实现
输出k层汉诺塔从x杆移动到y杆借助z杆的解法
将k-1层汉诺塔从x杆移动到z杆借助y杆
输出将k号圆盘从x移动到y
将k-1层汉诺塔从z杆移动到y杆借助x杆
1325:[例7.4] 循环比赛日程表
思路
可以发现规律,左上等于右下,右上等于左下把整个大矩阵分成最小的一块,也就是1个1,然后慢慢再合并成一个大矩阵
算法分析
从八位选手的循环比赛表中可以看出,这是一个具有对称性的方阵,可以把方阵一分为四来看,那么左上角的 4×4 的方阵就是前四位选手的循环比赛表,而右上角的 4*4 的方阵就是后四位选手的循环比赛表,它们在本质上是一样的,都是4 个选手的循环比赛表,所不同的只是选手编号不同而已,将左上角中方阵的所有元素加上 4 就能得到右上角的方阵。下方的两个方阵表示前四位选手和后四位选手进行交义循环比赛的情况,同样具有对称性,将右上角方阵复制到左下角即得到1、2、3、4 四位选手和 5、6、7、8 四位选手的循环比赛表,根据对称性,右下角的方阵应与左上角的方阵相同。这样,八名选手的循环比赛表可以由四名选手的循环比赛表根据对称性生成出来.同样地,四名选手的循环比赛表可以由二名选手的循环比赛表根据对称性生成出来,而两名选手的循环比赛表可以说是已知的,这种程序设计方法叫做分治法,其基本思想是把一个规模为 n 的问题分成若干个规模较小的问题,使得从这些较小问题的解易于构造出整个问题的解。
棋子移动1
思路
根据样例可以发现4,5(n,n+1).9,10(2n+1,2n+2); 第二行的右边第一行的左边。第二 行的 左边第一行右边都是-1
当n>4时我们尽量让n递归到4。
每当n>4的时候就会多出来两行。



















 上海工商
上海工商