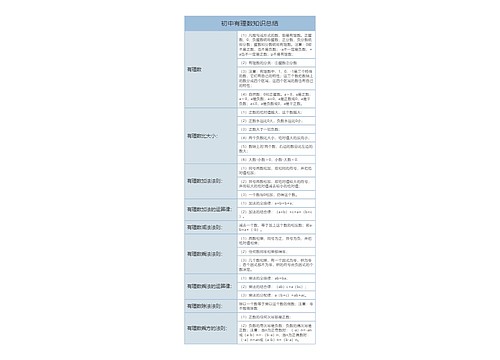
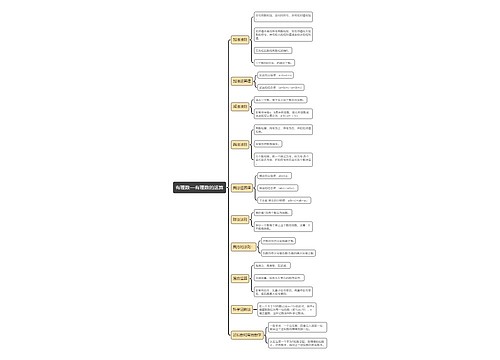
利润极值问题快速破解有诀窍思维导图

经济利润问题中涉及到函数求极值的题型在省国考行测考察中是小伙伴比较头疼的一类问题,往往不知道如何快速找出解题的突破口,最终只得望洋兴叹。
树图思维导图提供 利润极值问题快速破解有诀窍 在线思维导图免费制作,点击“编辑”按钮,可对 利润极值问题快速破解有诀窍 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4a7ed7ae784f9c02b9aa42ef002bf070
思维导图大纲
利润极值问题快速破解有诀窍思维导图模板大纲
经济利润问题中涉及到函数求极值的题型在省国考行测考察中是小伙伴比较头疼的一类问题,往往不知道如何快速找出解题的突破口,最终只得望洋兴叹。为了破解这个瓶颈,找到解题的切入点,这里梳理了完备快捷的解题思路,针对不同的类型对症下药,使得这类问题有章可循,有法可解。
1.考查题型梳理,快速定位识别
考查一般分为两种类型,都是涉及到总利润最大值的求解。关于总利润值的数学表达式跟产品数量与单件利润直接相关,故而总利润这个变量可以通过这两类量进行表示。第一种类型,告知销售某种商品,可以通过降价提高销售数量,并不直接提供总利润的函数表达式,需要我们建立,最终表示的形式是一元二次函数;而第二种则是,提供总利润关于销售数量的函数表达式,这里往往是一元多次函数(一元三次函数频次最高)。
2.量身定做钥匙,高效精确破解
针对题型一,根据总利润=产品数量脳单个利润,快速建立关于总利润的函数表达式,这里建立的一元二次函数不建议小伙伴们用配方法找最大值,计算量大耗时耗力,这里考虑抛物线的两点式进行求解会更便捷。可以把一元二次函数化成抛物线两点式的标准形式y=a(x-x1)(x-x2),当就是取极值点的位置,a>0时,取最小值,如下图所示;a<0时,取最大值。
针对题型二,给出总利润关于销售数量的函数表达式,这里一般均是一元三次函数,解决的途径是进行一次求导,令求导的函数等于0,解出未知量的值。这时算出的结果就是取极值的位置,至于是极大值或是极小值,涉及单调升降,那就需要求二阶导,但没有必要,我们这里求出的值就是我们所要求的结果。
3.例题精讲
【例1】某商品的进货单价为80元,销售单价为100元,每天可售出120件,已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元 B.6元
C.7元 D.8元
【解析】本题涉及经济利润问题中总利润最大值的求解,没有直接给出函数表达式,需要我们自己建立。先设销售单价应降低的金额是x元,根据总利润=产品数量脳单件利润,总利润用y表示,则有y=(100-80-x)(120+20x),这里化成抛物线两点式的标准形式y=a(x-x1)(x-x2)=-20(x-20)(x+6),x1=20,x2=-6,当就是取极值点位置,由于a<0,故而此时最大值,满足的选项为C。
【例2】某企业的净利润y(单位:10万元)与产量x(单位:100万件)之间的关系为:问该企业的净利润的最大值是多少万元?
A.5 B.50
C.60 D.70
【解析】很明显,这里给出了总利润的一元三次函数表达式,按照解题流程对其求出一阶导,令,解得(舍去),当x=2时,取极值,故考虑到利润的单位为10万元,所以最大利润值为5脳10=50万元,满足的选项为B。
通过两道经典例题,我们做个总结:遇到经济利润问题中涉及求解利润最值的问题,首先能够学会快速定位匹配题型,根据不同的类型选用合适的解题流程去求解,建立函数表达式要准确,求解导数更要细心,这些基础工作不能纰漏,环环相扣,强化练习,加以时日,解决这部分问题时定能得心应手。

















 上海工商
上海工商