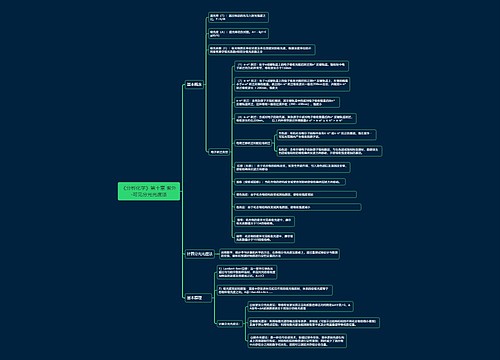
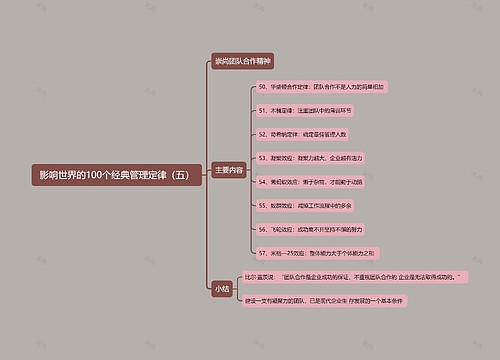
资料分析知识点分享-给定效率型思维导图

工程问题在国考中属于常考知识点,在近5年国考中,每年会考到,因此,我们还是应该对此知识点多做练习。对于工程问题主要分为三大类:给定时间型、给定效率型、条件综合型。今天我们主要就给定效率型给大家做以介绍。
树图思维导图提供 资料分析知识点分享-给定效率型 在线思维导图免费制作,点击“编辑”按钮,可对 资料分析知识点分享-给定效率型 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:baccdc281d6cffd2cb0e0412778ced68
思维导图大纲
资料分析知识点分享-给定效率型思维导图模板大纲
工程问题在国考中属于常考知识点,在近5年国考中,每年会考到,因此,我们还是应该对此知识点多做练习。对于工程问题主要分为三大类:给定时间型、给定效率型、条件综合型。今天我们主要就给定效率型给大家做以介绍。
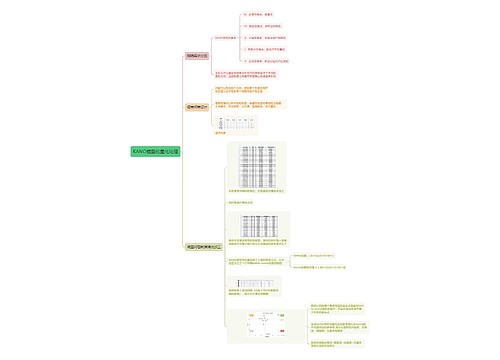
题型识别
题干中可以直接或间接找到不同主体之间的效率比
方法技巧
根据效率比赋效率
根据赋的效率和时间求工作总量
根据已知条件问啥求啥
三、例题精讲
【例1】某单位甲、乙、丙三人负责整理一项档案,他们工作5天完成了1/4,之后甲和乙因其他工作被调离,两天后才返回,期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2,则完成这项工作共需要花费( )天。
A.20
B.21
C.22
D.23
【答案】C
【解析】由于题干中直接给出了甲、乙、丙三人的工作效率之比,为给定效率型工程问题。
第一步,赋效率,根据甲、乙、丙三人的工作效率之比为4:3:2,赋甲的效率为4、乙的效率为3、丙的效率为2。
第二步,求总量,根据"甲、乙、丙三人负责整理一项档案,他们工作5天完成了1/4"得 1/4工作总量=(4+3+2)脳5,即 1/4 工作总量=9脳5,可得工作总量=180。
第三步,问啥求啥,设甲乙返回后三人合作共干了x天,列方程得9脳5+2脳2+9x=180,解得x=14+ ,即甲乙返回后三人合作15天干完了此工程,所以完成此项工程花费总时间为5+2+15=22(天)。
因此,选择C选项。
【例2】有甲、乙、丙三个工作组,已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天,再由乙、丙组共同工作7天,正好完成。如果三组共同完成,需要整7天。B工程如丙组单独完成正好需要10天,问如由甲、乙组共同完成,需要多少天?
A.不到6天
B.6天多
C.7天多
D.超过8天
【答案】C
【解析】由"乙组2天的工作量与甲、丙共同工作1天的工作量相同"得2乙=甲+丙,由"甲、乙组共同工作3天,再由乙、丙组共同工作7天,正好完成。如果三组共同完成,需要整7天"得3(甲+乙)+7(乙+丙)=7(甲+乙+丙),化简得甲、乙、丙三者效率之间的关系甲:乙:丙=3:4:5,由此判断本题为间接给出效率比型工程问题。
第一步,赋效率,根据甲:乙:丙=3:4:5赋甲的效率为3,乙的效率为4,丙的效率为5。
第二步,求总量,B工程总量=10丙=10脳5=50。
第三步,问啥求啥,甲、乙共同完成时间=,即需要7天多完成。
因此,选择C选项。
四、小结
对于给定效率型工程问题做题时要注意直接给出效率比还是间接给出,直接给出好判断,间接给出需要根据已知条件进行判断,看是否可推出效率之间的关系。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 辊压断带分析 在线思维导图免费制作,点击“编辑”按钮,可对 辊压断带分析 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:55fdf0827fa2a220b0b4047d75df5032






 上海工商
上海工商