备战2022年国考,数量高频考点你知多少?思维导图

华图教育带领大家学习国考中数量的高频考点,让同学们“对症下药”,掌握高频考点。
树图思维导图提供 备战2022年国考,数量高频考点你知多少? 在线思维导图免费制作,点击“编辑”按钮,可对 备战2022年国考,数量高频考点你知多少? 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4bfc6f439bd917ce9b3babafbd33ef27
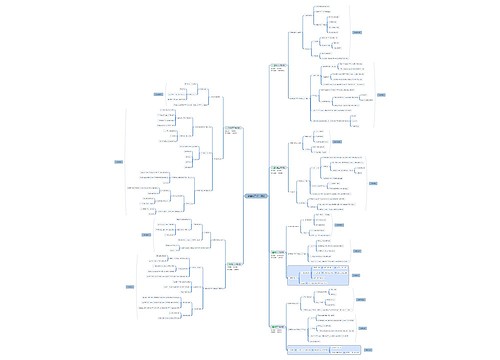
思维导图大纲
备战2022年国考,数量高频考点你知多少?思维导图模板大纲
俗话说得好:"光阴似箭,日月如梭"。一年一度的国考近在咫尺,我相信很多同学已经开始摩拳擦掌备战2022国考,但是光有一腔热血是不够的,因此只有了解并掌握国考中的高频考点才会在千军万马中脱颖而出,那么今天华图老师带领大家学习国考中数量的高频考点,让同学们"对症下药",掌握高频考点。
第一个高频考点是工程问题。工程问题在我们日常生活中也是处处可见的,例如盖楼,修桥,铺路等等,总之就是在一定的时间内完成一定的工作总量,因此工程问题的核心公式为:。另外当工作效率一定时,工作总量与工作时间呈正比例;当工作时间一定时,工作总量与工作效率呈正比例;当工作总量一定时,工作效率与工作时间呈反比例。而且满足的形式,那么可以运用赋值法进行解题,一般用于给定时间型与效率制约性。方程法也同样适用于工程问题,利用题中给出的已知量列方程求未知量。工程问题在国考中难度较为简单,但并不是一步可以出结果的题目,大多是考察综合分析能力。
接下来是环形相遇与追及问题,我们可以将校园中的操场作为一个环形相遇与追及问题模型。环形相遇的题型特征是环形跑道,背向而行,主要核心公式:;另一个则是环形追及问题,环形追及题型特征是环形跑道,同向而行,主要核心公式:。相遇追及问题干货华图老师已经传授给同学们了,那么请同学们思考一下,直线型n次相遇公式和环形n次相遇和追及公式是什么呢?
第三个高频考点就是排列组合与概率。排列组合与概率问题在国考数量关系中是重点也是难点,首先同学们需要了解两大原理,分别是加法原理与乘法原理。加法原理:若完成一件事,可以根据某个条件分为几种情况,各种情况都能独立完成此项任务,则将多种情况计算出的结果相加,所得的和为完成这件事情的种类数;乘法原理则是:若完成一件事情,需要划分为多种步骤依次完成,每个步骤内的任务之间没有交叉,则将每个步骤计算出的结果相乘,所得的积为完成这件事情的种类数。我们来举一个例子:若我们要乘坐交通工具从北京前往广州,有几种到达方式?那么交通方式可以有高铁、飞机、火车,那么一共有3种到达方式,运用的是加法原理,因为这3种交通方式相互独立完成。我们将题目进行变动一下:若我们要乘坐交通工具从北京前往广州并且要求途中必须要经过青岛,有几种到达方式?那么我们可以乘坐火车或是飞机从北京到青岛,再从青岛可以乘坐船、高铁、飞机到达广州,那么一共有2脳3=6种到达方式。其中。然而考试不可能仅仅考察我们排列与组合的计算能力,因此我们需要掌握解决排列组合的技巧与方法。这里面华图老师给大家总结了五种技巧与方法:1.捆绑法2.插空法3隔板法4.错位排列5.环形排列。其中隔板法,错位排列,环形排列较为特殊。隔板法的特征是将n个相同元素分配给m个单位至少得一个,解题技巧为;错位排列的特征是n个元素,n个位置,不归原位,通俗来讲就是将n个元素的位置打乱并重新排序,
国考数量关系中的主要高频考点需要同学们牢牢掌握,只有了解考试的侧重点,才能在考试中脱颖而出,还需要同学们从题海中悟出知识点的真谛,从而拥有举一反三的学习能力。华图教育 李秋辰
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 销售经理半年规划 在线思维导图免费制作,点击“编辑”按钮,可对 销售经理半年规划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:e614d6bcf03e9318109240a18697c5d1


















 上海工商
上海工商