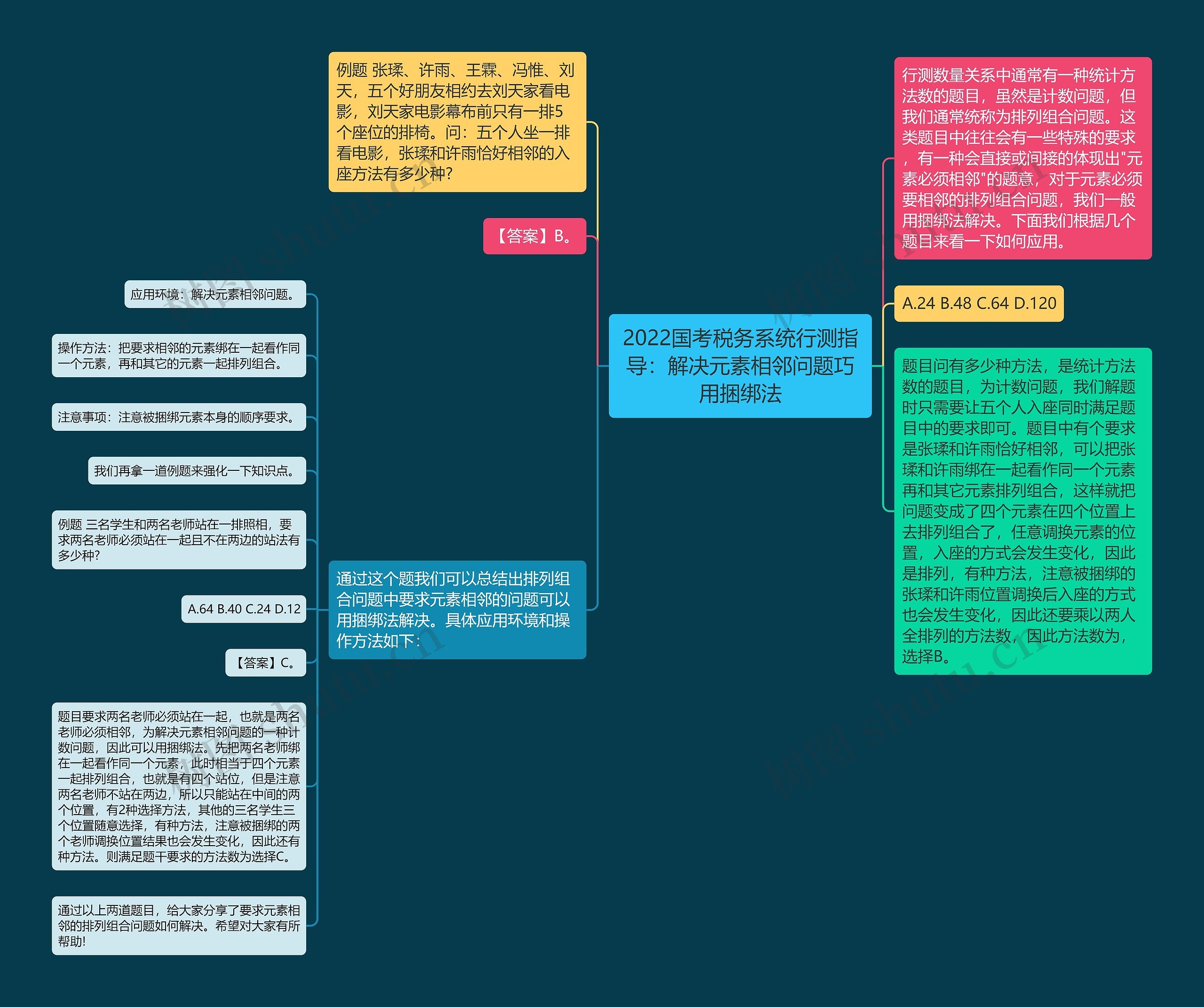
2022国考税务系统行测指导：解决元素相邻问题巧用捆绑法思维导图
华图教育为大家整理了行测备考相关知识供广大考生复习，更多备考技巧请持续关注华图教育。
树图思维导图提供 2022国考税务系统行测指导：解决元素相邻问题巧用捆绑法 在线思维导图免费制作，点击“编辑”按钮，可对 2022国考税务系统行测指导：解决元素相邻问题巧用捆绑法 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：741e8a305cccbdbb6f65442ff89fd4fa
思维导图大纲
2022国考税务系统行测指导：解决元素相邻问题巧用捆绑法思维导图模板大纲
行测数量关系中通常有一种统计方法数的题目，虽然是计数问题，但我们通常统称为排列组合问题。这类题目中往往会有一些特殊的要求，有一种会直接或间接的体现出"元素必须相邻"的题意，对于元素必须要相邻的排列组合问题，我们一般用捆绑法解决。下面我们根据几个题目来看一下如何应用。
例题 张瑈、许雨、王霖、冯惟、刘天，五个好朋友相约去刘天家看电影，刘天家电影幕布前只有一排5个座位的排椅。问：五个人坐一排看电影，张瑈和许雨恰好相邻的入座方法有多少种?
A.24 B.48 C.64 D.120
【答案】B。
题目问有多少种方法，是统计方法数的题目，为计数问题，我们解题时只需要让五个人入座同时满足题目中的要求即可。题目中有个要求是张瑈和许雨恰好相邻，可以把张瑈和许雨绑在一起看作同一个元素再和其它元素排列组合，这样就把问题变成了四个元素在四个位置上去排列组合了，任意调换元素的位置，入座的方式会发生变化，因此是排列，有种方法，注意被捆绑的张瑈和许雨位置调换后入座的方式也会发生变化，因此还要乘以两人全排列的方法数，因此方法数为，选择B。
通过这个题我们可以总结出排列组合问题中要求元素相邻的问题可以用捆绑法解决。具体应用环境和操作方法如下：
应用环境：解决元素相邻问题。
操作方法：把要求相邻的元素绑在一起看作同一个元素，再和其它的元素一起排列组合。
注意事项：注意被捆绑元素本身的顺序要求。
我们再拿一道例题来强化一下知识点。
例题 三名学生和两名老师站在一排照相，要求两名老师必须站在一起且不在两边的站法有多少种?
A.64 B.40 C.24 D.12
【答案】C。
题目要求两名老师必须站在一起，也就是两名老师必须相邻，为解决元素相邻问题的一种计数问题，因此可以用捆绑法。先把两名老师绑在一起看作同一个元素，此时相当于四个元素一起排列组合，也就是有四个站位，但是注意两名老师不站在两边，所以只能站在中间的两个位置，有2种选择方法，其他的三名学生三个位置随意选择，有种方法，注意被捆绑的两个老师调换位置结果也会发生变化，因此还有种方法。则满足题干要求的方法数为选择C。
通过以上两道题目，给大家分享了要求元素相邻的排列组合问题如何解决。希望对大家有所帮助!
沪公网安备 31011502019485号
上海工商