初中数学知识点总结 一次函数思维导图
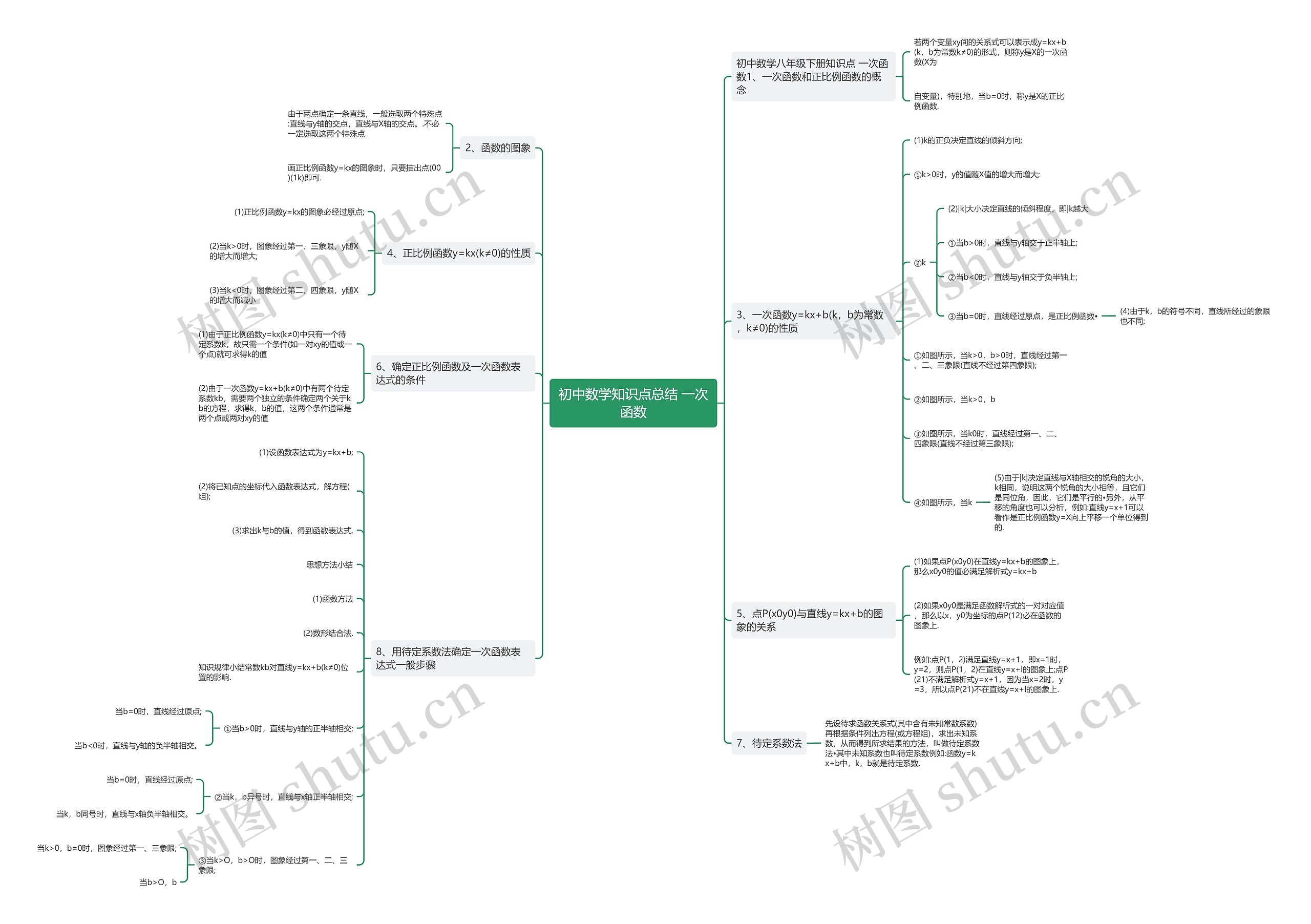
初中数学知识点总结一次函数思维导图包含以下内容:一次函数和正比例函数的概念,函数的图象的选取方法,一次函数的性质,包含他的倾斜方向、倾斜程度和所在象限,正比例函数的性质和图象特点,点与一次函数图象的关系,确定正比例函数和一次函数表达式的条件和待定系数法的应用,和数形结合法的思想方法,常数kb对直线位置的影响,如b=0时直线经过原点。
思维导图大纲
初中数学知识点总结 一次函数思维导图模板大纲
初中数学八年级下册知识点 一次函数1、一次函数和正比例函数的概念
若两个变量xy间的关系式可以表示成y=kx+b(k,b为常数k≠0)的形式,则称y是X的一次函数(X为
自变量),特别地,当b=0时,称y是X的正比例函数.
2、函数的图象
由于两点确定一条直线,一般选取两个特殊点:直线与y轴的交点,直线与X轴的交点。.不必一定选取这两个特殊点.
画正比例函数y=kx的图象时,只要描出点(00)(1k)即可.
3、一次函数y=kx+b(k,b为常数,k≠0)的性质
(1)k的正负决定直线的倾斜方向;
①k>0时,y的值随X值的增大而增大;
②k
(2)|k|大小决定直线的倾斜程度,即|k越大
①当b>0时,直线与y轴交于正半轴上;
②当b<0时,直线与y轴交于负半轴上;
③当b=0时,直线经过原点,是正比例函数•
(4)由于k,b的符号不同,直线所经过的象限也不同;
①如图所示,当k>0,b>0时,直线经过第一、二、三象限(直线不经过第四象限);
②如图所示,当k>0,b
③如图所示,当k0时,直线经过第一、二、四象限(直线不经过第三象限);
④如图所示,当k
(5)由于|k|决定直线与X轴相交的锐角的大小,k相同,说明这两个锐角的大小相等,且它们是同位角,因此,它们是平行的•另外,从平移的角度也可以分析,例如:直线y=x+1可以看作是正比例函数y=X向上平移一个单位得到的.
4、正比例函数y=kx(k≠0)的性质
(1)正比例函数y=kx的图象必经过原点;
(2)当k>0时,图象经过第一、三象限,y随X的增大而增大;
(3)当k<0时,图象经过第二、四象限,y随X的增大而减小
5、点P(x0y0)与直线y=kx+b的图象的关系
(1)如果点P(x0y0)在直线y=kx+b的图象上,那么x0y0的值必满足解析式y=kx+b
(2)如果x0y0是满足函数解析式的一对对应值,那么以x,y0为坐标的点P(12)必在函数的图象上.
例如:点P(1,2)满足直线y=x+1,即x=1时,y=2,则点P(1,2)在直线y=x+l的图象上;点P(21)不满足解析式y=x+1,因为当x=2时,y=3,所以点P(21)不在直线y=x+l的图象上.
6、确定正比例函数及一次函数表达式的条件
(1)由于正比例函数y=kx(k≠0)中只有一个待定系数k,故只需一个条件(如一对xy的值或一个点)就可求得k的值
(2)由于一次函数y=kx+b(k≠0)中有两个待定系数kb,需要两个独立的条件确定两个关于kb的方程,求得k,b的值,这两个条件通常是两个点或两对xy的值
7、待定系数法
先设待求函数关系式(其中含有未知常数系数)再根据条件列出方程(或方程组),求出未知系数,从而得到所求结果的方法,叫做待定系数法•其中未知系数也叫待定系数例如:函数y=kx+b中,k,b就是待定系数.
8、用待定系数法确定一次函数表达式一般步骤
(1)设函数表达式为y=kx+b;
(2)将已知点的坐标代入函数表达式,解方程(组);
(3)求出k与b的值,得到函数表达式.
思想方法小结
(1)函数方法
(2)数形结合法.
知识规律小结常数kb对直线y=kx+b(k≠0)位置的影响.
①当b>0时,直线与y轴的正半轴相交;
当b=0时,直线经过原点;
当b<0时,直线与y轴的负半轴相交。
②当k,b异号时,直线与x轴正半轴相交;
当b=0时,直线经过原点;
当k,b同号时,直线与x轴负半轴相交。
③当k>O,b>O时,图象经过第一、二、三象限;
当k>0,b=0时,图象经过第一、三象限;
当b>O,b
相关思维导图模板

树图思维导图提供 初中数学知识点:函数的知识总结 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学知识点:函数的知识总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2d00dc959c5f7231397b5bddbd27bc38

树图思维导图提供 初中中考数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 初中中考数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1faad0bb5d25debdd93164c6f235227b


















 上海工商
上海工商