行测知识点(一)思维导图
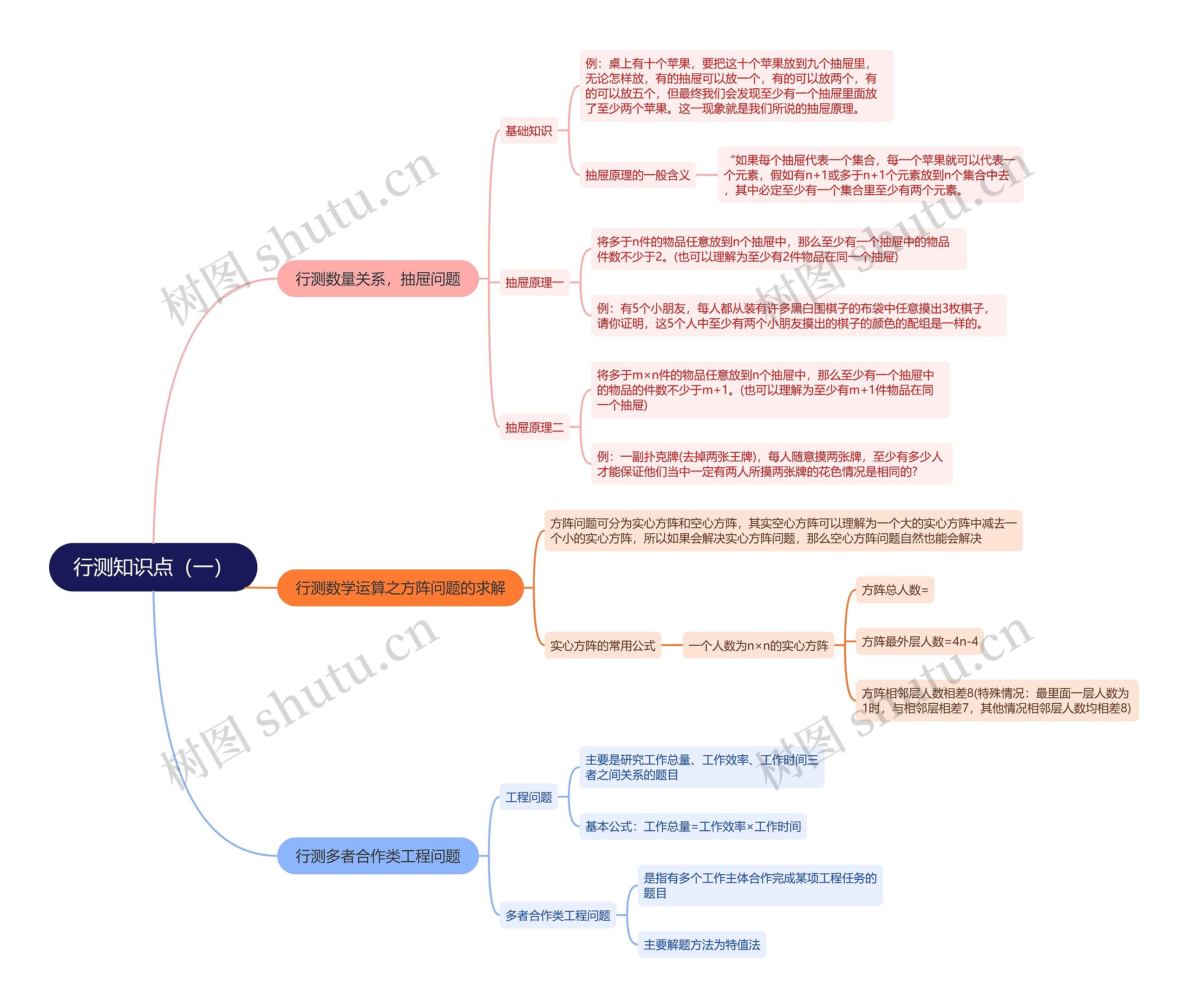
行测数量关系,抽屉问题;行测数学运算之方阵问题的求解;行测多者合作类工程问题,三个知识点概要描写
树图思维导图提供 行测知识点(一) 在线思维导图免费制作,点击“编辑”按钮,可对 行测知识点(一) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d04a55e52085f62166292fe3960c4788
思维导图大纲
行测知识点(一)思维导图模板大纲
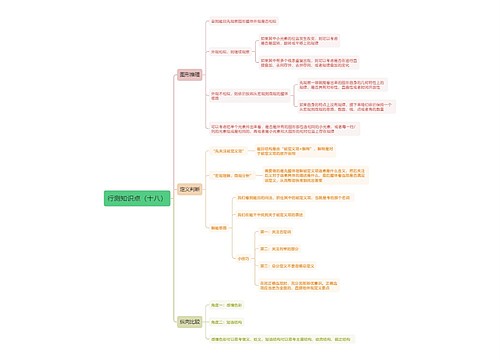
行测数量关系,抽屉问题
基础知识
例:桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,有的抽屉可以放一个,有的可以放两个,有的可以放五个,但最终我们会发现至少有一个抽屉里面放了至少两个苹果。这一现象就是我们所说的抽屉原理。
抽屉原理的一般含义
“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一个集合里至少有两个元素。
抽屉原理一
将多于n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品件数不少于2。(也可以理解为至少有2件物品在同一个抽屉)
例:有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子,请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
抽屉原理二
将多于m×n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品的件数不少于m+1。(也可以理解为至少有m+1件物品在同一个抽屉)
例:一副扑克牌(去掉两张王牌),每人随意摸两张牌,至少有多少人才能保证他们当中一定有两人所摸两张牌的花色情况是相同的?
行测数学运算之方阵问题的求解
方阵问题可分为实心方阵和空心方阵,其实空心方阵可以理解为一个大的实心方阵中减去一个小的实心方阵,所以如果会解决实心方阵问题,那么空心方阵问题自然也能会解决
实心方阵的常用公式
一个人数为n×n的实心方阵
方阵总人数=
方阵最外层人数=4n-4
方阵相邻层人数相差8(特殊情况:最里面一层人数为1时,与相邻层相差7,其他情况相邻层人数均相差8)
行测多者合作类工程问题
工程问题
主要是研究工作总量、工作效率、工作时间三者之间关系的题目
基本公式:工作总量=工作效率×工作时间
多者合作类工程问题
是指有多个工作主体合作完成某项工程任务的题目
主要解题方法为特值法
相关思维导图模板
树图思维导图提供 行测知识点(二十三) 在线思维导图免费制作,点击“编辑”按钮,可对 行测知识点(二十三) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:939865d088306f44ddbfd5c253baa737
树图思维导图提供 行测知识点(二十二) 在线思维导图免费制作,点击“编辑”按钮,可对 行测知识点(二十二) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:dc47b7a895f0eee8e0e9f333eaf0d0f6










 上海工商
上海工商