读书笔记《西方宏观经济学》经济增长思维导图
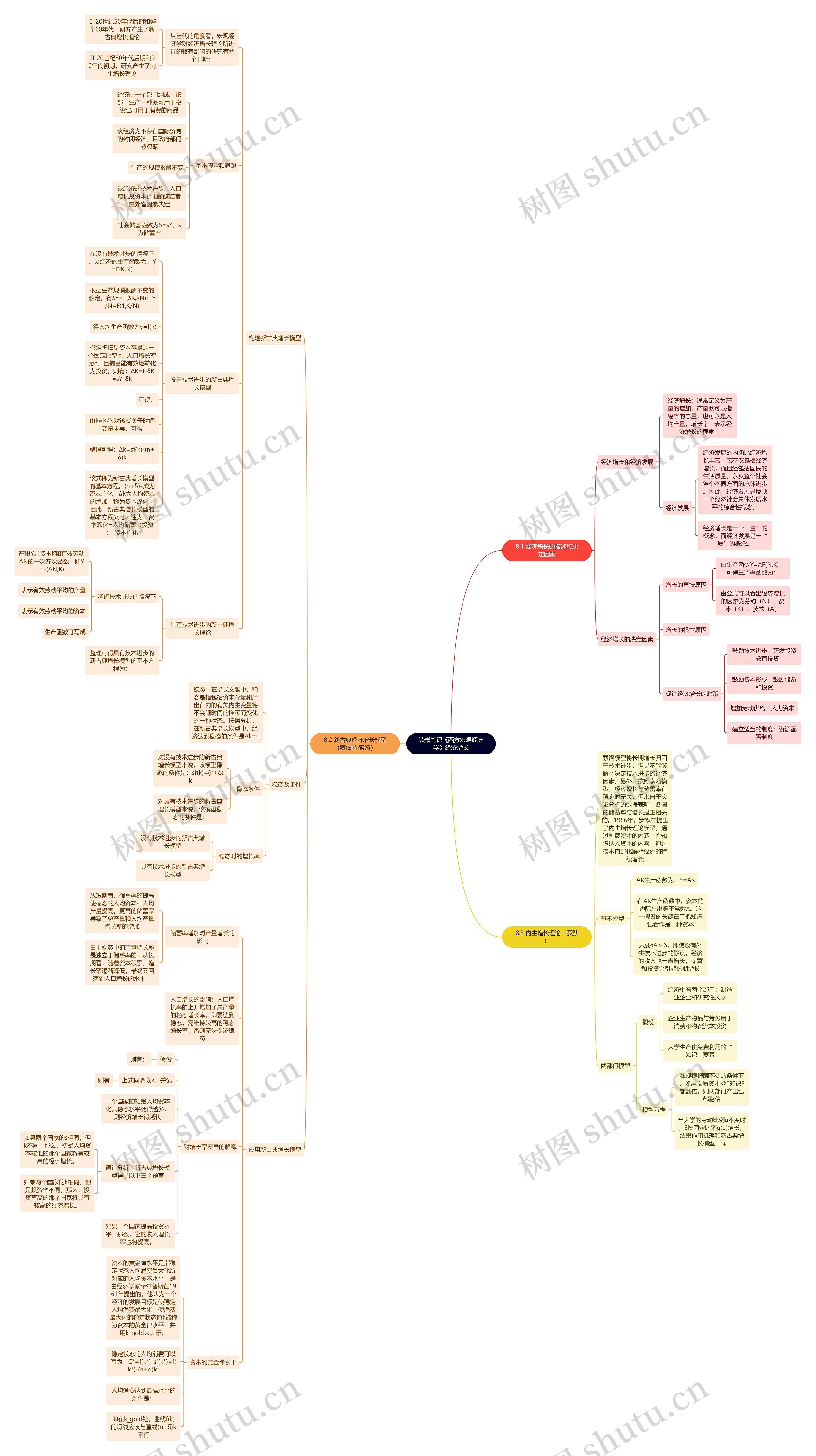
《西方宏观经济学》经济增长的概述
树图思维导图提供 读书笔记《西方宏观经济学》经济增长 在线思维导图免费制作,点击“编辑”按钮,可对 读书笔记《西方宏观经济学》经济增长 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:fe92a12b31043deb601f74347f2f4a74
思维导图大纲
读书笔记《西方宏观经济学》经济增长思维导图模板大纲
8.1 经济增长的描述和决定因素
经济增长和经济发展
经济增长:通常定义为产量的增加,产量既可以指经济的总量,也可以是人均产量。增长率:表示经济增长的程度。
经济发展
经济发展的内涵比经济增长丰富,它不仅包括经济增长,而且还包括国民的生活质量,以及整个社会各个不同方面的总体进步。因此,经济发展是反映一个经济社会总体发展水平的综合性概念。
经济增长是一个“量”的概念,而经济发展是一“质”的概念。
经济增长的决定因素
增长的直接原因
由生产函数Y=AF(N,K),可得生产率函数为:
由公式可以看出经济增长的因素为劳动(N)、资本(K)、技术(A)
增长的根本原因
促进经济增长的政策
鼓励技术进步:研发投资、教育投资
鼓励资本形成:鼓励储蓄和投资
增加劳动供给:人力资本
建立适当的制度:资源配置制度
8.2 新古典经济增长模型(罗伯特·索洛)
构建新古典增长模型
从当代的角度看,宏观经济学对经济增长理论所进行的较有影响的研宄有两个时期:
Ⅰ.20世纪50年代后期和整个60年代,研宄产生了新古典增长理论
Ⅱ.20世纪80年代后期和90年代初期,研宄产生了内生增长理论
基本假定和思路
经济由一个部门组成,该部门生产一种既可用于投资也可用于消费的商品
该经济为不存在国际贸易的封闭经济,且政府部门被忽略
生产的规模报酬不变
该经济的技术进步、人口增长及资本折旧的速度都由外省因素决定
社会储蓄函数为S=sY,s为储蓄率
没有技术进步的新古典增长模型
在没有技术进步的情况下,该经济的生产函数为:Y=F(K,N)
根据生产规模报酬不变的假定,有λY=F(λK,λN):Y/N=F(1,K/N)
得人均生产函数为y=f(k)
假定折旧是资本存量的一个固定比率σ,人口增长率为n,且储蓄能有效地转化为投资,则有:ΔK=I-δK=sY-δK
可得:
由k=K/N对该式关于时间变量求导,可得
整理可得:Δk=sf(k)-(n+δ)k
该式即为新古典增长模型的基本方程。(n+δ)k成为资本广化;Δk为人均资本的增加,称为资本深化。因此,新古典增长模型的基本方程又可表述为:资本深化=人均储蓄(投资)-资本广化
具有技术进步的新古典增长理论
考虑技术进步的情况下
产出Y是资本K和有效劳动AN的一次齐次函数,即Y=F(AN,K)
表示有效劳动平均的产量
表示有效劳动平均的资本
生产函数可写成
整理可得具有技术进步的新古典增长模型的基本方程为:
稳态及条件
稳态:在增长文献中,稳态是指包括资本存量和产出在内的有关内生变量将不会随时间的推移而变化的一种状态。按照分析,在新古典增长模型中,经济达到稳态的条件是Δk=0
稳态条件
对没有技术进步的新古典增长模型来说,该模型稳态的条件是:sf(k)=(n+δ)k
对具有技术进步的新古典增长模型来说,该模型稳态的条件是:
稳态时的增长率
没有技术进步的新古典增长模型
具有技术进步的新古典增长模型
应用新古典增长模型
储蓄率增加对产量增长的影响
从短期看,储蓄率的提高使稳态的人均资本和人均产量提高;更高的储蓄率导致了总产量和人均产量增长率的增加
由于稳态中的产量增长率是独立于储蓄率的,从长期看,随着资本积累,增长率逐渐降低,最终又回落到人口增长的水平。
人口增长的影响:人口增长率的上升增加了总产量的稳态增长率。即要达到稳态,需维持较高的稳态增长率,否则无法保证稳态
对增长率差异的解释
假设
则有:
上式同除以k,并记
则有
一个国家的初始人均资本比其稳态水平低得越多,则经济增长得越快
通过分析,新古典增长模型得出以下三个预言
如果两个国家的s相同,但k不同,那么,初始人均资本较低的那个国家将有较高的经济增长。
如果两个国家的k相同,但是投资率不同,那么,投资率高的那个国家将具有较高的经济增长。
如果一个国家提高投资水平,那么,它的收入增长率也将提高。
资本的黄金律水平
资本的黄金律水平是指稳定状态人均消费最大化所对应的人均资本水平,是由经济学家菲尔普斯在1961年提出的。他认为一个经济的发展目标是使稳定人均消费最大化。使消费最大化的稳定状态值k被称为资本的黄金律水平,并用k_gold来表示。
稳定状态的人均消费可以写为:C*=f(k*)-sf(k*)=f(k*)-(n+δ)k*
人均消费达到最高水平的条件是:
即在k_gold处,曲线f(k)的切线应该与直线(n+δ)k平行
8.3 内生增长理论(罗默)
索洛模型将长期增长归因于技术进步,但是不能够解释决定技术进步的经济因素。另外,按照索洛模型,经济增长与储蓄率在稳态时无关,但来自于实证分析的数据表明:各国的储蓄率与增长是正相关的。1986年,罗默在提出了内生增长理论模型,通过扩展资本的内涵,将知识纳入资本的内容,通过技术内部化解释经济的持续增长
基本模型
AK生产函数为:Y=AK
在AK生产函数中,资本的边际产出等于常数A。这一假设的关键在于把知识也看作是一种资本
只要sA>δ,即使没有外生技术进步的假设,经济的收入也一直增长,储蓄和投资会引起长期增长
两部门模型
假设
经济中有两个部门:制造业企业和研究性大学
企业生产物品与劳务用于消费和物资资本投资
大学生产供免费利用的“知识”要素
模型方程
在规模报酬不变的条件下,如果物质资本K和知识E都翻倍,则两部门产出也都翻倍
当大学的劳动比例u不变时,E按固定比率g(u)增长,结果作用机理和新古典增长模型一样










 上海工商
上海工商