读书笔记《西方微观经济学》 博弈论初步思维导图
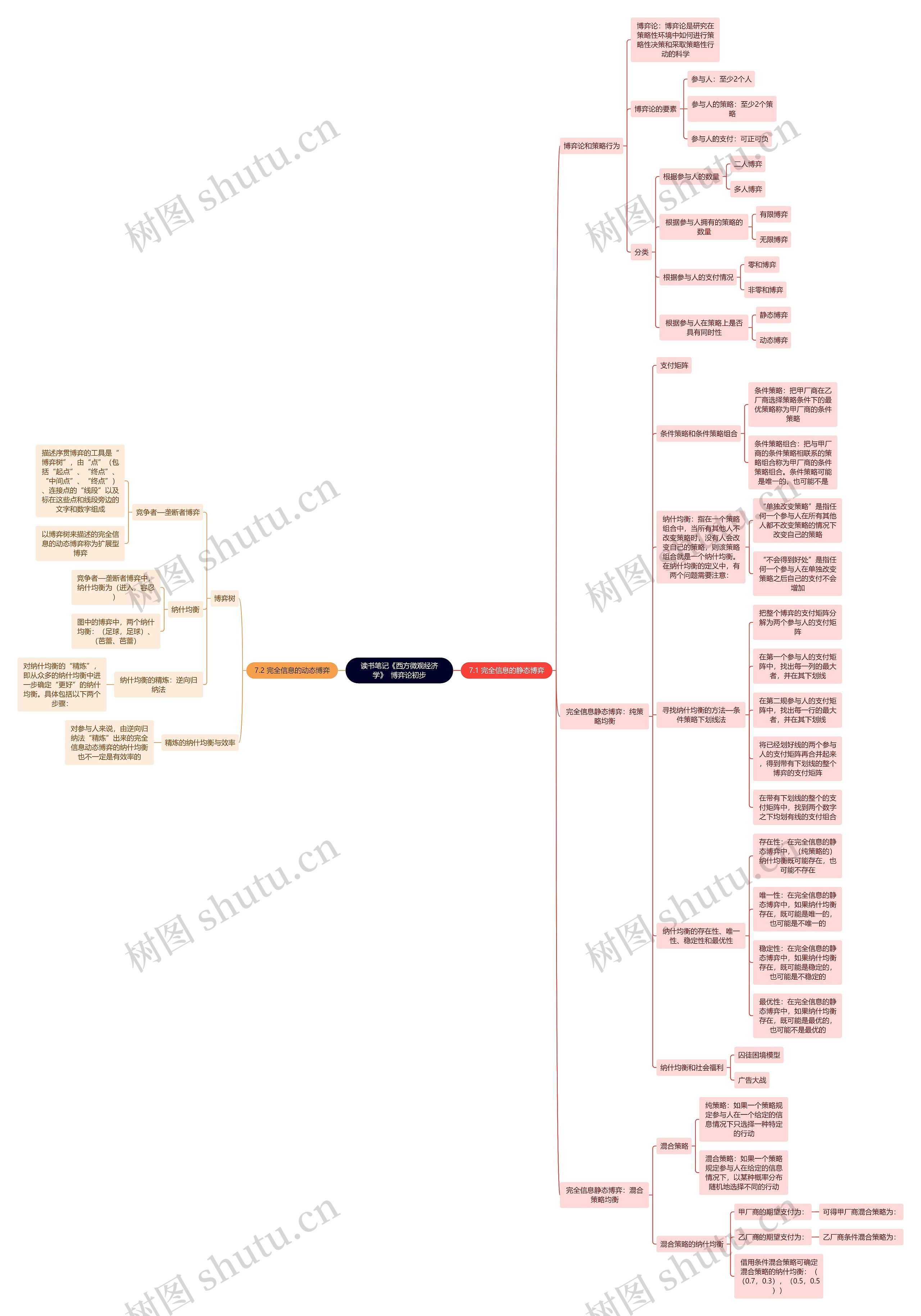
《西方微观经济学》 博弈论初步的概述
树图思维导图提供 读书笔记《西方微观经济学》 博弈论初步 在线思维导图免费制作,点击“编辑”按钮,可对 读书笔记《西方微观经济学》 博弈论初步 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4f4d1299971f6d77de160a6b9bbf7c8c
思维导图大纲
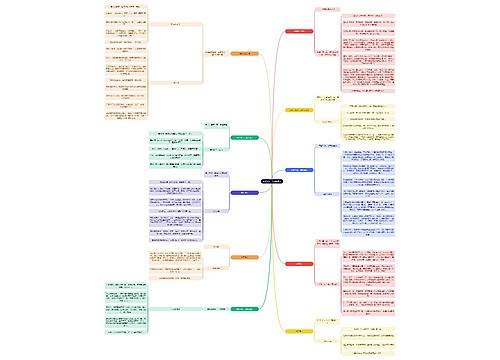
读书笔记《西方微观经济学》 博弈论初步思维导图模板大纲
7.1 完全信息的静态博弈
博弈论和策略行为
博弈论:博弈论是研究在策略性环境中如何进行策略性决策和采取策略性行动的科学
博弈论的要素
参与人:至少2个人
参与人的策略:至少2个策略
参与人的支付:可正可负
分类
根据参与人的数量
二人博弈
多人博弈
根据参与人拥有的策略的数量
有限博弈
无限博弈
根据参与人的支付情况
零和博弈
非零和博弈
根据参与人在策略上是否具有同时性
静态博弈
动态博弈
完全信息静态博弈:纯策略均衡
支付矩阵
条件策略和条件策略组合
条件策略:把甲厂商在乙厂商选择策略条件下的最优策略称为甲厂商的条件策略
条件策略组合:把与甲厂商的条件策略相联系的策略组合称为甲厂商的条件策略组合。条件策略可能是唯一的,也可能不是
纳什均衡:指在一个策略组合中,当所有其他人不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。在纳什均衡的定义中,有两个问题需要注意:
“单独改变策略”是指任何一个参与人在所有其他人都不改变策略的情况下改变自己的策略
“不会得到好处”是指任何一个参与人在单独改变策略之后自己的支付不会增加
寻找纳什均衡的方法—条件策略下划线法
把整个博弈的支付矩阵分解为两个参与人的支付矩阵
在第一个参与人的支付矩阵中,找出每一列的最大者,并在其下划线
在第二规参与人的支付矩阵中,找出每一行的最大者,并在其下划线
将已经划好线的两个参与人的支付矩阵再合并起来,得到带有下划线的整个博弈的支付矩阵
在带有下划线的整个的支付矩阵中,找到两个数字之下均划有线的支付组合
纳什均衡的存在性、唯一性、稳定性和最优性
存在性:在完全信息的静态博弈中,(纯策略的)纳什均衡既可能存在,也可能不存在
唯一性:在完全信息的静态博弈中,如果纳什均衡存在,既可能是唯一的,也可能是不唯一的
稳定性:在完全信息的静态博弈中,如果纳什均衡存在,既可能是稳定的,也可能是不稳定的
最优性:在完全信息的静态博弈中,如果纳什均衡存在,既可能是最优的,也可能不是最优的
纳什均衡和社会福利
囚徒困境模型
广告大战
完全信息静态博弈:混合策略均衡
混合策略
纯策略:如果一个策略规定参与人在一个给定的信息情况下只选择一种特定的行动
混合策略:如果一个策略规定参与人在给定的信息情况下,以某种概率分布随机地选择不同的行动
混合策略的纳什均衡
甲厂商的期望支付为:
可得甲厂商混合策略为:
乙厂商的期望支付为:
乙厂商条件混合策略为:
借用条件混合策略可确定混合策略的纳什均衡:((0.7,0.3),(0.5,0.5))
7.2 完全信息的动态博弈
博弈树
竞争者—垄断者博弈
描述序贯博弈的工具是“博弈树”,由“点”(包括“起点”、“终点”、“中间点”、“终点”)、连接点的“线段”以及标在这些点和线段旁边的文字和数字组成
以博弈树来描述的完全信息的动态博弈称为扩展型博弈
纳什均衡
竞争者—垄断者博弈中,纳什均衡为(进入,容忍)
图中的博弈中,两个纳什均衡:(足球,足球)、(芭蕾、芭蕾)
纳什均衡的精炼:逆向归纳法
对纳什均衡的“精炼”,即从众多的纳什均衡中进一步确定“更好”的纳什均衡。具体包括以下两个步骤:
精炼的纳什均衡与效率
对参与人来说,由逆向归纳法“精炼”出来的完全信息动态博弈的纳什均衡也不一定是有效率的
相关思维导图模板

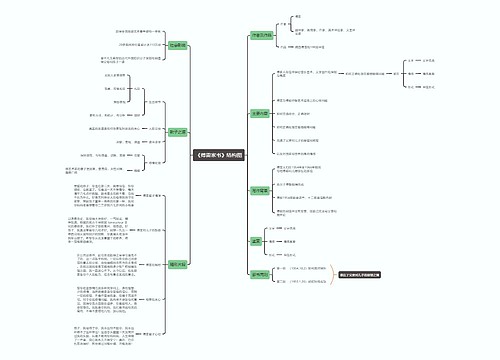
树图思维导图提供 西方的圣经翻译 在线思维导图免费制作,点击“编辑”按钮,可对 西方的圣经翻译 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:3104fe3824be64e52b77d4076c31fce8


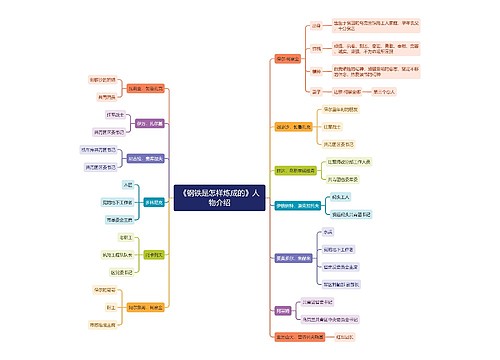
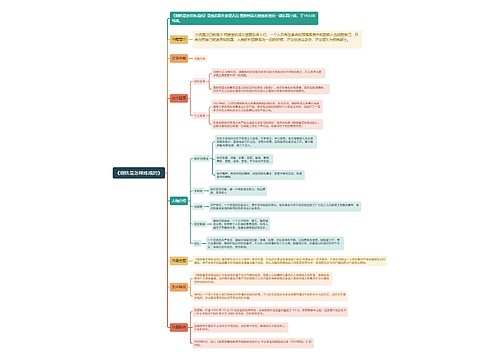
树图思维导图提供 <a id="_Toc29876"></a> 在线思维导图免费制作,点击“编辑”按钮,可对 <a id="_Toc29876"></a> 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:749b6db5aac596c21518016ea382b6c7








 上海工商
上海工商