初中数学一元一次方程知识点总结思维导图
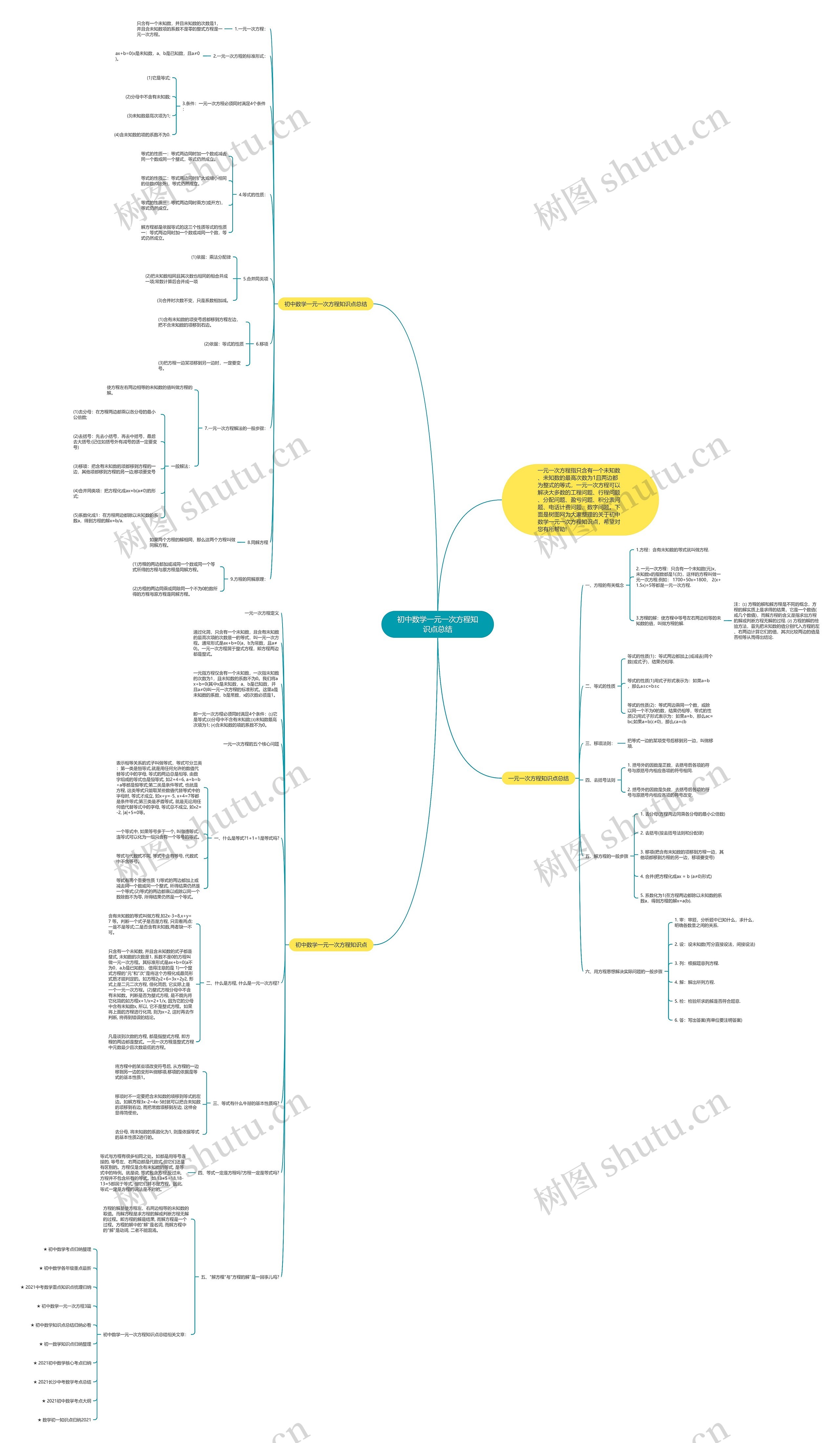
初中数学一元一次方程知识点总结思维导图包含以下几点:一元一次方程定义、标准形式、条件、等式的性质、合并同类项、移项、一元一次方程解法的一般步骤、同解方程和方程的同解原理。解方程的一般步骤包含去分母、去括号、移项、合并同类项和系数化为1,用方程思想解决实际问题的一般步骤包含审题、设未知数、列方程、解方程、检验和写出答案,一元一次方程可以解决大多数的工程问题、行程问题、分配问题、盈亏问题、积分表问题、电话计费问题、数字问题。
思维导图大纲
初中数学一元一次方程知识点总结思维导图模板大纲
一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式,一元一次方程可以解决大多数的工程问题、行程问题、分配问题、盈亏问题、积分表问题、电话计费问题、数字问题。下面是树图网为大家整理的关于初中数学一元一次方程知识点,希望对您有所帮助!
初中数学一元一次方程知识点总结
1.一元一次方程:
只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。
2.一元一次方程的标准形式:
ax+b=0(x是未知数,a、b是已知数,且a≠0)。
3.条件:一元一次方程必须同时满足4个条件:
(1)它是等式;
(2)分母中不含有未知数;
(3)未知数最高次项为1;
(4)含未知数的项的系数不为0.
4.等式的性质:
等式的性质一:等式两边同时加一个数或减去同一个数或同一个整式,等式仍然成立。
等式的性质二:等式两边同时扩大或缩小相同的倍数(0除外),等式仍然成立。
等式的性质三:等式两边同时乘方(或开方),等式仍然成立。
解方程都是依据等式的这三个性质等式的性质一:等式两边同时加一个数或减同一个数,等式仍然成立。
5.合并同类项
(1)依据:乘法分配律
(2)把未知数相同且其次数也相同的相合并成一项;常数计算后合并成一项
(3)合并时次数不变,只是系数相加减。
6.移项
(1)含有未知数的项变号后都移到方程左边,把不含未知数的项移到右边。
(2)依据:等式的性质
(3)把方程一边某项移到另一边时,一定要变号。
7.一元一次方程解法的一般步骤:
使方程左右两边相等的未知数的值叫做方程的解。
一般解法:
(1)去分母:在方程两边都乘以各分母的最小公倍数;
(2)去括号:先去小括号,再去中括号,最后去大括号;(记住如括号外有减号的话一定要变号)
(3)移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边;移项要变号
(4)合并同类项:把方程化成ax=b(a≠0)的形式;
(5)系数化成1:在方程两边都除以未知数的系数a,得到方程的解x=b/a.
8.同解方程
如果两个方程的解相同,那么这两个方程叫做同解方程。
9.方程的同解原理:
(1)方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。
(2)方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程。
一元一次方程知识点总结
一、方程的有关概念
1.方程:含有未知数的等式就叫做方程.
2. 一元一次方程:只含有一个未知数(元)x,未知数x的指数都是1(次),这样的方程叫做一元一次方程.例如: 1700+50x=1800, 2(x+1.5x)=5等都是一元一次方程.
3.方程的解:使方程中等号左右两边相等的未知数的值,叫做方程的解.
注:⑴ 方程的解和解方程是不同的概念,方程的解实质上是求得的结果,它是一个数值(或几个数值),而解方程的含义是指求出方程的解或判断方程无解的过程. ⑵ 方程的解的检验方法,首先把未知数的值分别代入方程的左、右两边计算它们的值,其次比较两边的值是否相等从而得出结论.
二、等式的性质
等式的性质(1):等式两边都加上(或减去)同个数(或式子),结果仍相等.
等式的性质(1)用式子形式表示为:如果a=b,那么a±c=b±c
等式的性质(2):等式两边乘同一个数,或除以同一个不为0的数,结果仍相等,等式的性质(2)用式子形式表示为:如果a=b,那么ac=bc;如果a=b(c≠0),那么ca=cb
三、移项法则:
把等式一边的某项变号后移到另一边,叫做移项.
四、去括号法则
1. 括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
2. 括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号改变.
五、解方程的一般步骤
1. 去分母(方程两边同乘各分母的最小公倍数)
2. 去括号(按去括号法则和分配律)
3. 移项(把含有未知数的项移到方程一边,其他项都移到方程的另一边,移项要变号)
4. 合并(把方程化成ax = b (a≠0)形式)
5. 系数化为1(在方程两边都除以未知数的系数a,得到方程的解x=a(b).
六、用方程思想解决实际问题的一般步骤
1. 审:审题,分析题中已知什么,求什么,明确各数量之间的关系.
2. 设:设未知数(可分直接设法,间接设法)
3. 列:根据题意列方程.
4. 解:解出所列方程.
5. 检:检验所求的解是否符合题意.
6. 答:写出答案(有单位要注明答案)
初中数学一元一次方程知识点
一元一次方程定义
通过化简,只含有一个未知数,且含有未知数的最高次项的次数是一的等式,叫一元一次方程。通常形式是ax+b=0(a,b为常数,且a≠0)。一元一次方程属于整式方程,即方程两边都是整式。
一元指方程仅含有一个未知数,一次指未知数的次数为1,且未知数的系数不为0。我们将ax+b=0(其中x是未知数,a、b是已知数,并且a≠0)叫一元一次方程的标准形式。这里a是未知数的系数,b是常数,x的次数必须是1。
即一元一次方程必须同时满足4个条件:⑴它是等式;⑵分母中不含有未知数;⑶未知数最高次项为1; ⑷含未知数的项的系数不为0。
一元一次方程的五个核心问题
一、什么是等式?1+1=1是等式吗?
表示相等关系的式子叫做等式,等式可分三类:第一类是恒等式,就是用任何允许的数值代替等式中的字母, 等式的两边总是相等, 由数字组成的等式也是恒等式, 如2+4=6, a+b=b+a等都是恒等式;第二类是条件等式, 也就是方程, 这类等式只能取某些数值代替等式中的字母时, 等式才成立, 如x+y=-5, x+4=7等都是条件等式;第三类是矛盾等式, 就是无论用任何值代替等式中的字母, 等式总不成立, 如x2=-2, |a|+5=0等。
一个等式中, 如果等号多于一个, 叫做连等式,连等式可以化为一组只含有一个等号的等式。
等式与代数式不同, 等式中含有等号, 代数式中不含等号。
等式有两个重要性质 1)等式的两边都加上或减去同一个数或同一个整式, 所得结果仍然是一个等式;(2)等式的两边都乘以或除以同一个数除数不为零, 所得结果仍然是一个等式。
二、什么是方程, 什么是一元一次方程?
含有未知数的等式叫做方程,如2x-3=8,x+y=7 等。判断一个式子是否是方程, 只需看两点:一是不是等式;二是否含有未知数,两者缺一不可。
只含有一个未知数, 并且含未知数的式子都是整式, 未知数的次数是1, 系数不是0的方程叫做一元一次方程。其标准形式是ax+b=0(a不为0,a,b是已知数),值得注意的是 1)一个整式方程的"元"和"次"是将这个方程化成最简形式后才能判定的。如方程2y2+6=3x+2y2, 形式上是二元二次方程, 但化简后, 它实际上是一个一元一次方程。(2)整式方程分母中不含有未知数。判断是否为整式方程, 是不能先将它化简的如方程x+1/x=2+1/x, 因为它的分母中含有未知数x, 所以, 它不是整式方程。如果将上面的方程进行化简, 则为x=2, 这时再去作判断, 将得到错误的结论。
凡是谈到次数的方程, 都是指整式方程, 即方程的两边都是整式。一元一次方程是整式方程中元数最少且次数最低的方程。
三、等式有什么牛掰的基本性质吗?
将方程中的某些项改变符号后, 从方程的一边移到另一边的变形叫做移项,移项的依据是等式的基本性质1。
移项时不一定要把含未知数的项移到等式的左边。如解方程3x-2=4x-5时就可以把含未知数的项移到右边, 而把常数项移到左边, 这样会显得简便些。
去分母, 将未知数的系数化为1, 则是依据等式的基本性质2进行的。
四、等式一定是方程吗?方程一定是等式吗?
等式与方程有很多相同之处。如都是用等号连接的, 等号左、右两边都是代数式,但它们还是有区别的。方程仅是含有未知数的等式, 是等式中的特例。就是说, 等式包含方程;反过来, 方程并不包含所有的等式。如,13+5=18,18-13=5都属于等式, 但它们并不是方程。因此, 等式一定是方程的说法是不对的。
五、"解方程"与"方程的解"是一回事儿吗?
方程的解是使方程左、右两边相等的未知数的取值。而解方程是求方程的解或判断方程无解的过程。即方程的解是结果, 而解方程是一个过程。方程的解中的"解"是名词, 而解方程中的"解"是动词, 二者不能混淆。
初中数学一元一次方程知识点总结相关文章:
★ 初中数学考点归纳整理
★ 初中数学各年级重点最新
★ 2021中考数学重点知识点梳理归纳
★ 初中数学一元一次方程3篇
★ 初中数学知识点总结归纳必看
★ 初一数学知识点归纳整理
★ 2021初中数学核心考点归纳
★ 2021长沙中考数学考点总结
★ 2021初中数学考点大纲
★ 数学初一知识点归纳2021
相关思维导图模板

树图思维导图提供 初中数学知识点总结 一元一次方程 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学知识点总结 一元一次方程 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6cf7328eac5d822f76affb3c174315ff

树图思维导图提供 初中数学部分重要知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学部分重要知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f44dd68f05c835310401a7b5ff17650e

















 上海工商
上海工商