高三数学考试答题技巧和方法思维导图
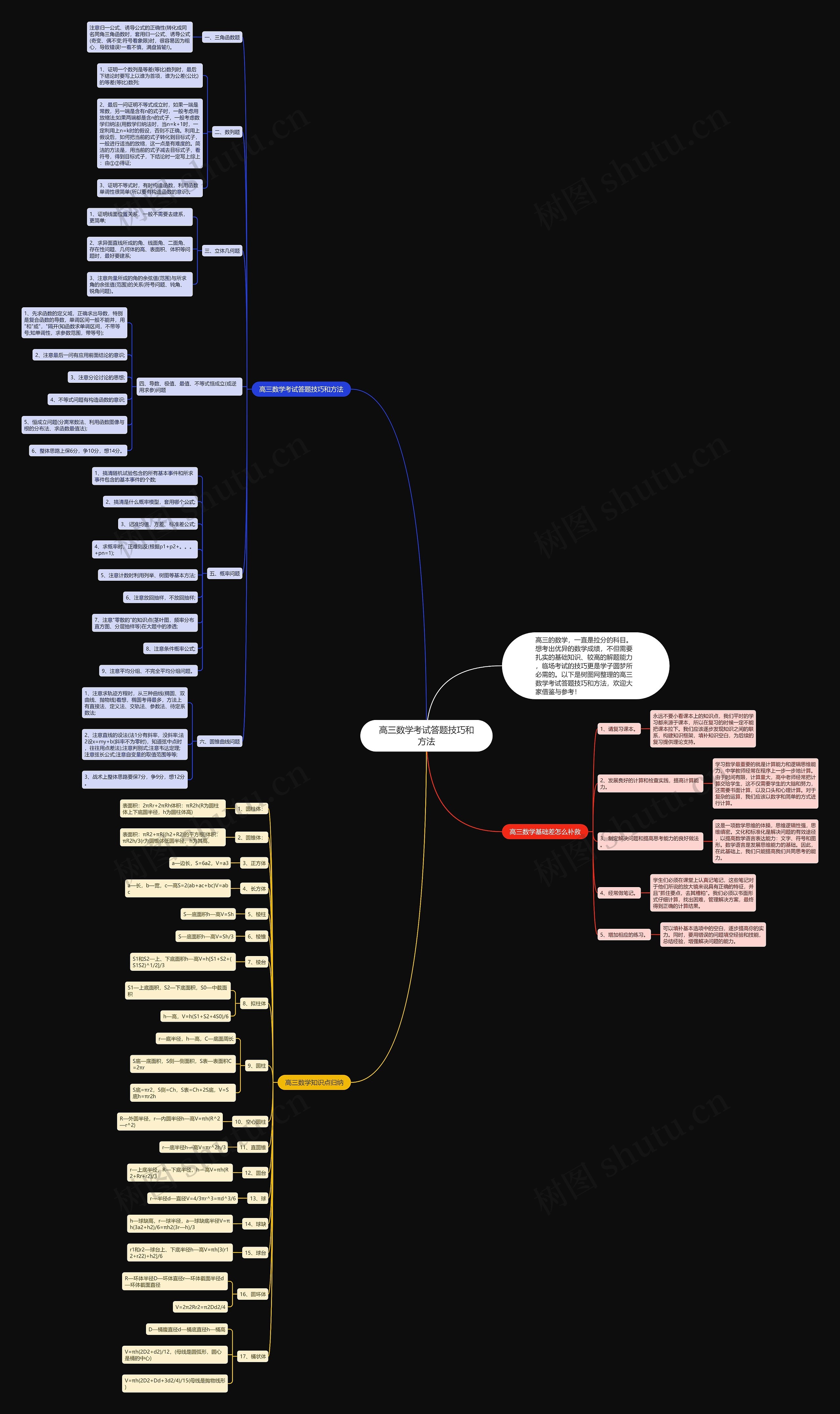
高三数学考试是让很多学生头疼的科目,不仅需要扎实的基础知识,高水平的解题能力,更需要临场考试的技巧,本模板提供了一些高三数学考试答题技巧和方法,包含三角函数、数列、立体几何、导数、极值、最值、不等式恒成立问题和概率问题等内容。解三角函数题需要注意归一公式、诱导公式的正确性,而证明等差数列和等比数列时需注明谁为首项、谁为公差或公比。在立体几何的题目中,建系有助于求解异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积和体积,针对导数、极值、最值、不等式恒成立和概率问题,本模板提供了详细解题思路和相关公式,掌握这些技巧和方法不仅可以在考场上发挥更好,也可以在平时练题中提高解题效率。
思维导图大纲
高三数学考试答题技巧和方法思维导图模板大纲
高三的数学,一直是拉分的科目。想考出优异的数学成绩,不但需要扎实的基础知识、较高的解题能力,临场考试的技巧更是学子圆梦所必需的。以下是树图网整理的高三数学考试答题技巧和方法,欢迎大家借鉴与参考!
高三数学考试答题技巧和方法
一、三角函数题
注意归一公式、诱导公式的正确性(转化成同名同角三角函数时,套用归一公式、诱导公式(奇变、偶不变;符号看象限)时,很容易因为粗心,导致错误!一着不慎,满盘皆输!)。
二、数列题
1、证明一个数列是等差(等比)数列时,最后下结论时要写上以谁为首项,谁为公差(公比)的等差(等比)数列;
2、最后一问证明不等式成立时,如果一端是常数,另一端是含有n的式子时,一般考虑用放缩法;如果两端都是含n的式子,一般考虑数学归纳法(用数学归纳法时,当n=k+1时,一定利用上n=k时的假设,否则不正确。利用上假设后,如何把当前的式子转化到目标式子,一般进行适当的放缩,这一点是有难度的。简洁的方法是,用当前的式子减去目标式子,看符号,得到目标式子,下结论时一定写上综上:由①②得证;
3、证明不等式时,有时构造函数,利用函数单调性很简单(所以要有构造函数的意识)。
三、立体几何题
1、证明线面位置关系,一般不需要去建系,更简单;
2、求异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积、体积等问题时,最好要建系;
3、注意向量所成的角的余弦值(范围)与所求角的余弦值(范围)的关系(符号问题、钝角、锐角问题)。
四、导数、极值、最值、不等式恒成立(或逆用求参)问题
1、先求函数的定义域,正确求出导数,特别是复合函数的导数,单调区间一般不能并,用"和"或","隔开(知函数求单调区间,不带等号;知单调性,求参数范围,带等号);
2、注意最后一问有应用前面结论的意识;
3、注意分论讨论的思想;
4、不等式问题有构造函数的意识;
5、恒成立问题(分离常数法、利用函数图像与根的分布法、求函数最值法);
6、整体思路上保6分,争10分,想14分。
五、概率问题
1、搞清随机试验包含的所有基本事件和所求事件包含的基本事件的个数;
2、搞清是什么概率模型,套用哪个公式;
3、记准均值、方差、标准差公式;
4、求概率时,正难则反(根据p1+p2+。。。+pn=1);
5、注意计数时利用列举、树图等基本方法;
6、注意放回抽样,不放回抽样;
7、注意"零散的"的知识点(茎叶图,频率分布直方图、分层抽样等)在大题中的渗透;
8、注意条件概率公式;
9、注意平均分组、不完全平均分组问题。
六、圆锥曲线问题
1、注意求轨迹方程时,从三种曲线(椭圆、双曲线、抛物线)着想,椭圆考得最多,方法上有直接法、定义法、交轨法、参数法、待定系数法;
2、注意直线的设法(法1分有斜率,没斜率;法2设x=my+b(斜率不为零时),知道弦中点时,往往用点差法);注意判别式;注意韦达定理;注意弦长公式;注意自变量的取值范围等等;
3、战术上整体思路要保7分,争9分,想12分。
高三数学基础差怎么补救
1、请复习课本。
永远不要小看课本上的知识点,我们平时的学习都来源于课本,所以在复习的时候一定不能把课本拉下。我们应该逐步发现知识之间的联系,构建知识框架,填补知识空白,为后续的复习提供理论支持。
2、发展良好的计算和检查实践,提高计算能力。
学习数学最重要的就是计算能力和逻辑思维能力,中学教师经常在程序上一步一步地计算。由于时间有限,计算量大,高中老师经常把计算交给学生,这不仅需要学生的大脑和努力,还需要书面计算,以及口头和心理计算。对于复杂的运算,我们应该以数字和简单的方式进行计算。
3、制定解决问题和提高思考能力的良好做法。
这是一项数学思维的体操,思维逻辑性强,思维缜密。文化和标准化是解决问题的有效途径,以提高数学语言表达能力:文字、符号和图形。数学语言是发展思维能力的基础。因此,在此基础上,我们只能提高我们共同思考的能力。
4、经常做笔记。
学生们必须在课堂上认真记笔记,这些笔记对于他们所说的放大镜来说具有正确的特征,并且"抓住要点,去其糟粕"。我们必须以书面形式仔细计算,找出困难,管理解决方案,最终得到正确的计算结果。
5、增加相应的练习。
可以填补基本选项中的空白,逐步提高你的实力。同时,要用错误的问题填空经验和技能,总结经验,增强解决问题的能力。
高三数学知识点归纳
1、圆柱体:
表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)
2、圆锥体:
表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高,
3、正方体
a—边长,S=6a2,V=a3
4、长方体
a—长,b—宽,c—高S=2(ab+ac+bc)V=abc
5、棱柱
S—底面积h—高V=Sh
6、棱锥
S—底面积h—高V=Sh/3
7、棱台
S1和S2—上、下底面积h—高V=h[S1+S2+(S1S2)^1/2]/3
8、拟柱体
S1—上底面积,S2—下底面积,S0—中截面积
h—高,V=h(S1+S2+4S0)/6
9、圆柱
r—底半径,h—高,C—底面周长
S底—底面积,S侧—侧面积,S表—表面积C=2πr
S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h
10、空心圆柱
R—外圆半径,r—内圆半径h—高V=πh(R^2—r^2)
11、直圆锥
r—底半径h—高V=πr^2h/3
12、圆台
r—上底半径,R—下底半径,h—高V=πh(R2+Rr+r2)/3
13、球
r—半径d—直径V=4/3πr^3=πd^3/6
14、球缺
h—球缺高,r—球半径,a—球缺底半径V=πh(3a2+h2)/6=πh2(3r—h)/3
15、球台
r1和r2—球台上、下底半径h—高V=πh[3(r12+r22)+h2]/6
16、圆环体
R—环体半径D—环体直径r—环体截面半径d—环体截面直径
V=2π2Rr2=π2Dd2/4
17、桶状体
D—桶腹直径d—桶底直径h—桶高
V=πh(2D2+d2)/12,(母线是圆弧形,圆心是桶的中心)
V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形)
相关思维导图模板

树图思维导图提供 高考数学考试答题技巧方法 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学考试答题技巧方法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:48743e9333ccf67d5a714e4d0f9310d4

树图思维导图提供 2022高中数学考试答题技巧 在线思维导图免费制作,点击“编辑”按钮,可对 2022高中数学考试答题技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:14f60b2df56374137ae149dd5d240be8













 上海工商
上海工商