有理数人教版数学初一上册教案思维导图
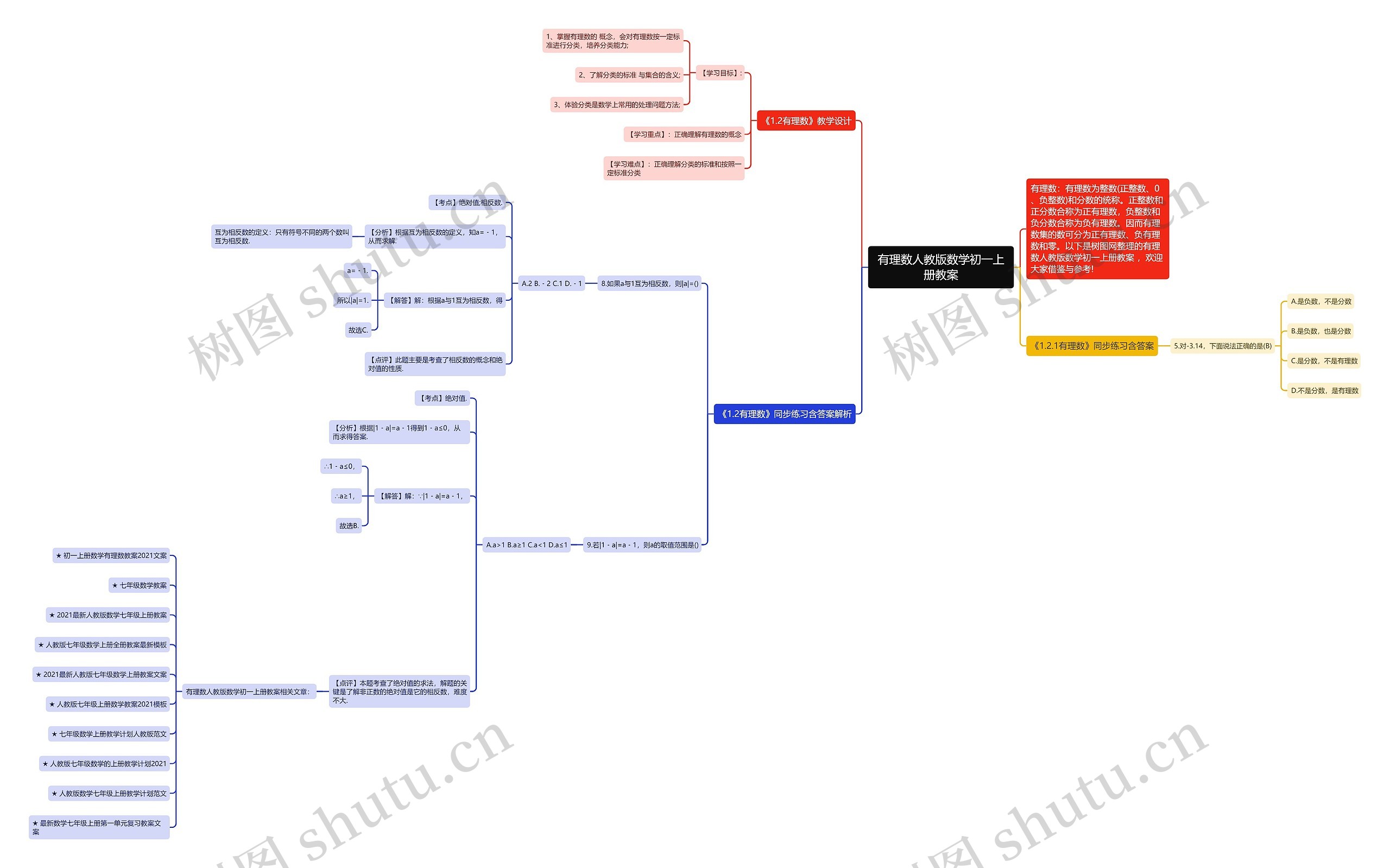
有理数的概念,即由整数和分数构成的数集,分为正有理数、负有理数和零,思维导图模板以《有理数人教版数学初一上册教案思维导图》为核心,对于初一上册有理数的教学内容进行了阐述,重点是掌握有理数的概念、分类标准和体验分类对问题解决的重要性,一些同步练习,并进行了题目分析和点评,包含到绝对值、相反数。
思维导图大纲
有理数人教版数学初一上册教案思维导图模板大纲
有理数:有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。以下是树图网整理的有理数人教版数学初一上册教案 ,欢迎大家借鉴与参考!
《1.2有理数》教学设计
【学习目标】:
1、掌握有理数的 概念,会对有理数按一定标准进行分类,培养分类能力;
2、了解分类的标准 与集合的含义;
3、体验分类是数学上常用的处理问题方法;
【学习重点】:正确理解有理数的概念
【学习难点】:正确理解分类的标准和按照一定标准分类
《1.2.1有理数》同步练习含答案
5.对-3.14,下面说法正确的是(B)
A.是负数,不是分数
B.是负数,也是分数
C.是分数,不是有理数
D.不是分数,是有理数
《1.2有理数》同步练习含答案解析
8.如果a与1互为相反数,则|a|=()
A.2 B.﹣2 C.1 D.﹣1
【考点】绝对值;相反数.
【分析】根据互为相反数的定义,知a=﹣1,从而求解.
互为相反数的定义:只有符号不同的两个数叫互为相反数.
【解答】解:根据a与1互为相反数,得
a=﹣1.
所以|a|=1.
故选C.
【点评】此题主要是考查了相反数的概念和绝对值的性质.
9.若|1﹣a|=a﹣1,则a的取值范围是()
A.a>1 B.a≥1 C.a<1 D.a≤1
【考点】绝对值.
【分析】根据|1﹣a|=a﹣1得到1﹣a≤0,从而求得答案.
【解答】解:∵|1﹣a|=a﹣1,
∴1﹣a≤0,
∴a≥1,
故选B.
【点评】本题考查了绝对值的求法,解题的关键是了解非正数的绝对值是它的相反数,难度不大.
有理数人教版数学初一上册教案相关文章:
★ 初一上册数学有理数教案2021文案
★ 七年级数学教案
★ 2021最新人教版数学七年级上册教案
★ 人教版七年级数学上册全册教案最新模板
★ 2021最新人教版七年级数学上册教案文案
★ 人教版七年级上册数学教案2021模板
★ 七年级数学上册教学计划人教版范文
★ 人教版七年级数学的上册教学计划2021
★ 人教版数学七年级上册教学计划范文
★ 最新数学七年级上册第一单元复习教案文案
相关思维导图模板

树图思维导图提供 有理数与无理数苏教版数学初一上册教案 在线思维导图免费制作,点击“编辑”按钮,可对 有理数与无理数苏教版数学初一上册教案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d3a555b91f6eca93616cad49443db249

树图思维导图提供 有理数的混合运算苏教版数学初一上册教案 在线思维导图免费制作,点击“编辑”按钮,可对 有理数的混合运算苏教版数学初一上册教案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f21bf02def572e575533102b4a02c3cf















 上海工商
上海工商