教师资格证数学常考知识点:相交线思维导图
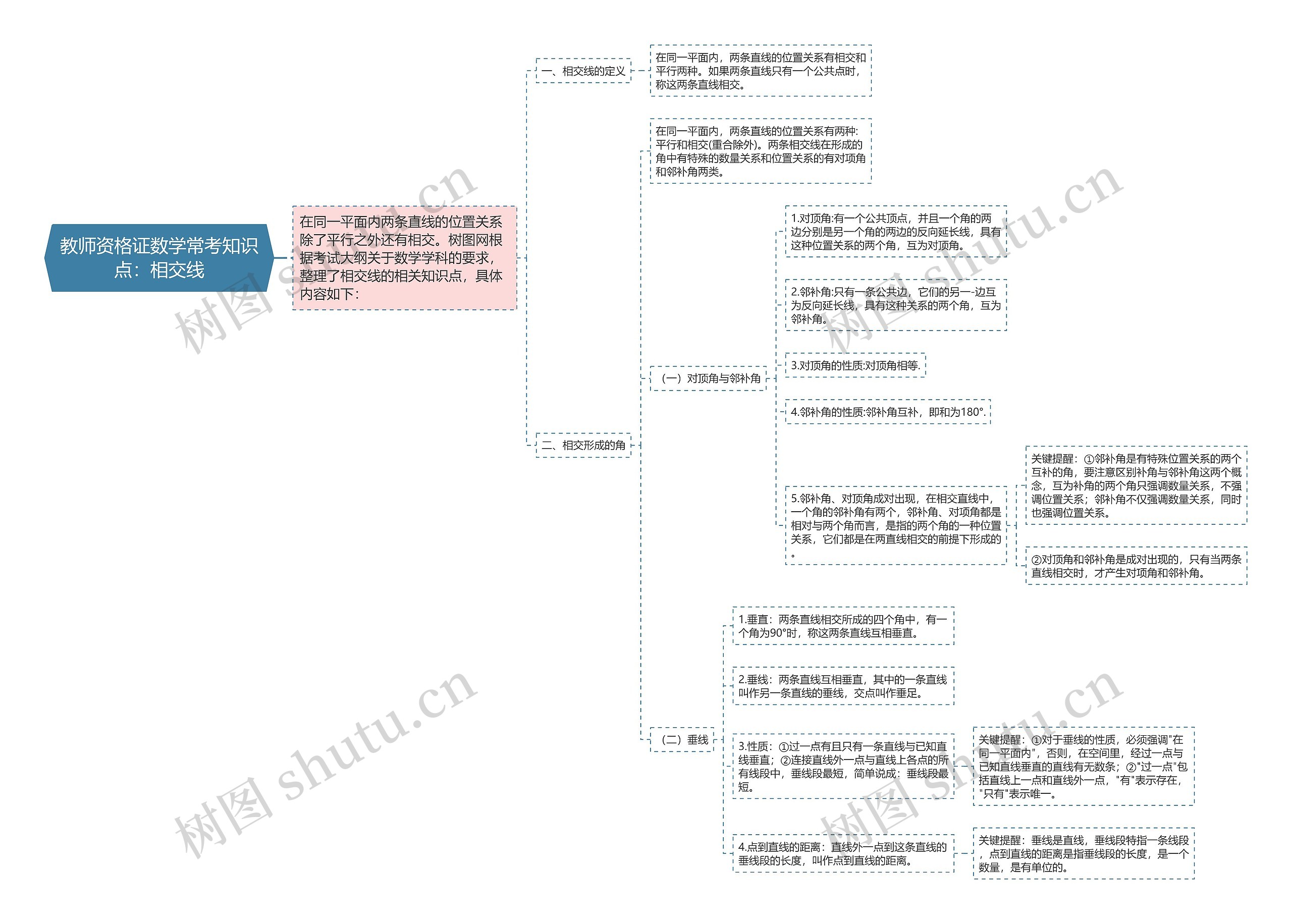
教师资格证数学常考知识点:相交线思维导图,是指在同一平面内,两条直线的位置关系除了平行之外,还有相交,两条相交线形成的角包含对项角和邻补角,对顶角相等,邻补角互补,垂直是指两条直线相交所成的四个角中有一个角为90°。垂线是两条垂直线中相互垂直的一条直线,性质是过一点有且只有一条直线与已知直线垂直,连接直线外一点与直线上各点的所有线段中,垂线段最短,点到直线的距离是直线外一点到本直线的垂线段的长度,要注意区分补角和邻补角的概念,只有当两条直线相交时,才产生对项角和邻补角。
思维导图大纲
教师资格证数学常考知识点:相交线思维导图模板大纲
在同一平面内两条直线的位置关系除了平行之外还有相交。树图网根据考试大纲关于数学学科的要求,整理了相交线的相关知识点,具体内容如下:
一、相交线的定义
在同一平面内,两条直线的位置关系有相交和平行两种。如果两条直线只有一个公共点时,称这两条直线相交。
二、相交形成的角
在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外)。两条相交线在形成的角中有特殊的数量关系和位置关系的有对项角和邻补角两类。
(一)对顶角与邻补角
1.对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
2.邻补角:只有一条公共边,它们的另一-边互为反向延长线,具有这种关系的两个角,互为邻补角。
3.对顶角的性质:对顶角相等.
4.邻补角的性质:邻补角互补,即和为180°.
5.邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个,邻补角、对项角都是相对与两个角而言,是指的两个角的一种位置关系,它们都是在两直线相交的前提下形成的。
关键提醒:①邻补角是有特殊位置关系的两个互补的角,要注意区别补角与邻补角这两个概念,互为补角的两个角只强调数量关系,不强调位置关系;邻补角不仅强调数量关系,同时也强调位置关系。
②对顶角和邻补角是成对出现的,只有当两条直线相交时,才产生对项角和邻补角。
(二)垂线
1.垂直:两条直线相交所成的四个角中,有一个角为90°时,称这两条直线互相垂直。
2.垂线:两条直线互相垂直,其中的一条直线叫作另一条直线的垂线,交点叫作垂足。
3.性质:①过一点有且只有一条直线与已知直线垂直;②连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短。
关键提醒:①对于垂线的性质,必须强调"在同一平面内",否则,在空间里,经过一点与已知直线垂直的直线有无数条;②"过一点"包括直线上一点和直线外一点,"有"表示存在,"只有"表示唯一。
4.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
关键提醒:垂线是直线,垂线段特指一条线段,点到直线的距离是指垂线段的长度,是一个数量,是有单位的。




















 上海工商
上海工商