百分数思维导图
六年级上册数学百分数相关内容的整理
树图思维导图提供 百分数 在线思维导图免费制作,点击“编辑”按钮,可对 百分数 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ecafd466c5f8cb14f5e28060a31df2bb
思维导图大纲
百分数思维导图模板大纲
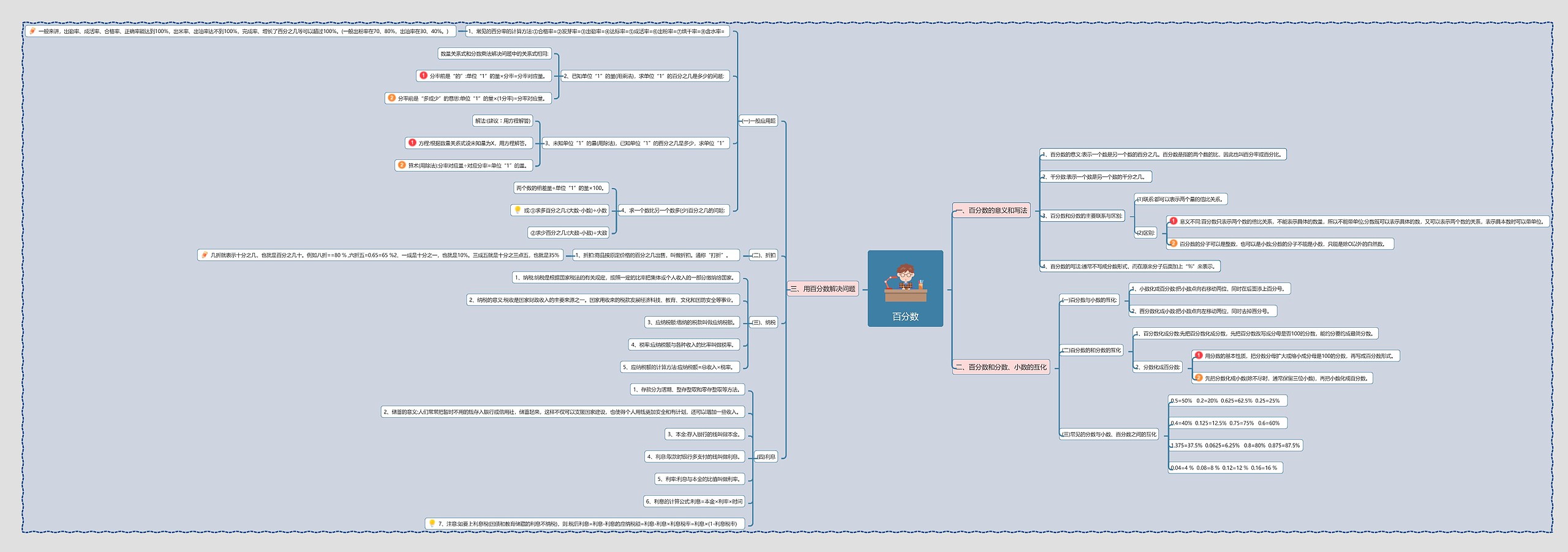
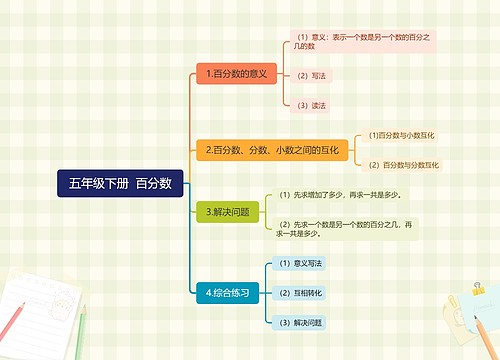
一、百分数的意义和写法
1、百分数的意义:表示一个数是另一个数的百分之几。百分数是指的两个数的比,因此也叫百分率或百分比。
2、千分数:表示一个数是另一个数的千分之几。
3、百分数和分数的主要联系与区别:
(1)联系:都可以表示两个量的倍比关系。
(2)区别:
意义不同:百分数只表示两个数的倍比关系,不能表示具体的数量,所以不能带单位;分数既可以表示具体的数,又可以表示两个数的关系,表示具本数时可以带单位。
百分数的分子可以是整数,也可以是小数;分数的分子不能是小数,只能是除O以外的自然数。
4、百分数的写法:通常不写成分数形式,而在原来分子后面加上“%”来表示。
二、百分数和分数、小数的互化
(一)百分数与小数的互化:
1、小数化成百分数:把小数点向右移动两位,同时在后面添上百分号。
2、百分数化成小数:把小数点向左移动两位,同时去掉百分号。
(二)百分数的和分数的互化
1、百分数化成分数:先把百分数化成分数,先把百分数改写成分母是否100的分数,能约分要约成最简分数。
2、分数化成百分数:
用分数的基本性质,把分数分母扩大或缩小成分母是100的分数,再写成百分数形式。
先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
(三)常见的分数与小数、百分数之间的互化
0.5=50% 0.2=20% 0.625=62.5% 0.25=25%
0.4=40% 0.125=12.5% 0.75=75% 0.6=60%
1.375=37.5% 0.0625=6.25% 0.8=80% 0.875=87.5%
0.04=4 % 0.08=8 % 0.12=12 % 0.16=16 %
三、用百分数解决问题
(一)一般应用题
1、常见的百分率的计算方法:①合格率=②发芽率=③出勤率=④达标率=⑤成活率=⑥出粉率=⑦烘干率=⑧含水率=
一般来讲,出勤率、成活率、合格率、正确率能达到100%,出米率、出油率达不到100%,完成率、增长了百分之几等可以超过100%。(一般出粉率在70、80%,出油率在30、40%。)
2、已知单位“1”的量(用乘法),求单位“1”的百分之几是多少的问题:
数量关系式和分数乘法解决问题中的关系式相同:
分率前是“的”:单位“1”的量×分率=分率对应量。
分率前是“多或少”的意思:单位“1”的量×(1分率)=分率对应量。
3、未知单位“1”的量(用除法),已知单位“1”的百分之几是多少,求单位“1”
解法:(建议︰用方程解答)
方程:根据数量关系式设未知量为X,用方程解答。
算术(用除法):分率对应量÷对应分率=单位“1”的量。
4、求一个数比另一个数多(少)百分之几的问题:
两个数的相差量÷单位“1”的量×100。
或:①求多百分之几:(大数-小数)÷小数
②求少百分之几:(大数-小数)÷大数
(二)、折扣
1、折扣:商品按原定价格的百分之几出售,叫做折扣。通称“打折”。
几折就表示十分之几,也就是百分之几十。例如八折==80 % ,六折五=0.65=65 %2、一成是十分之一,也就是10%。三成五就是十分之三点五,也就是35%
(三)、纳税
1、纳税:纳税是根据国家税法的有关规定,按照一定的比率把集体或个人收入的一部分缴纳给国家。
2、纳税的意义:税收是国家财政收入的主要来源之一。国家用收来的税款发展经济科技、教育、文化和国防安全等事业。
3、应纳税额:缴纳的税款叫做应纳税额。
4、税率:应纳税额与各种收入的比率叫做税率。
5、应纳税额的计算方法:应纳税额=总收入×税率。
(四)利息
1、存款分为活期、整存整取和零存整取等方法。
2、储蓄的意义:人们常常把暂时不用的钱存入银行或信用社,储蓄起来,这样不仅可以支援国家建设,也使得个人用钱更加安全和有计划,还可以增加一些收入。
3、本金:存入银行的钱叫做本金。
4、利息:取款时银行多支付的钱叫做利息。
5、利率:利息与本金的比值叫做利率。
6、利息的计算公式:利息=本金×利率×时间
7、注意:如要上利息税(国债和教育储藏的利息不纳税),则:税后利息=利息-利息的应纳税额=利息-利息×利息税率=利息×(1-利息税率)


















 上海工商
上海工商