高一数学教案：交集与并集(5)思维导图
教案通常又叫教学设计，包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等。树图网为大家整理了《高一数学教案：交集与并集(5)》，供大家参考。
树图思维导图提供 高一数学教案：交集与并集(5) 在线思维导图免费制作，点击“编辑”按钮，可对 高一数学教案：交集与并集(5) 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：bd8b42034b84cf39176465e465d2cc3c
思维导图大纲
高一数学教案：交集与并集(5)思维导图模板大纲
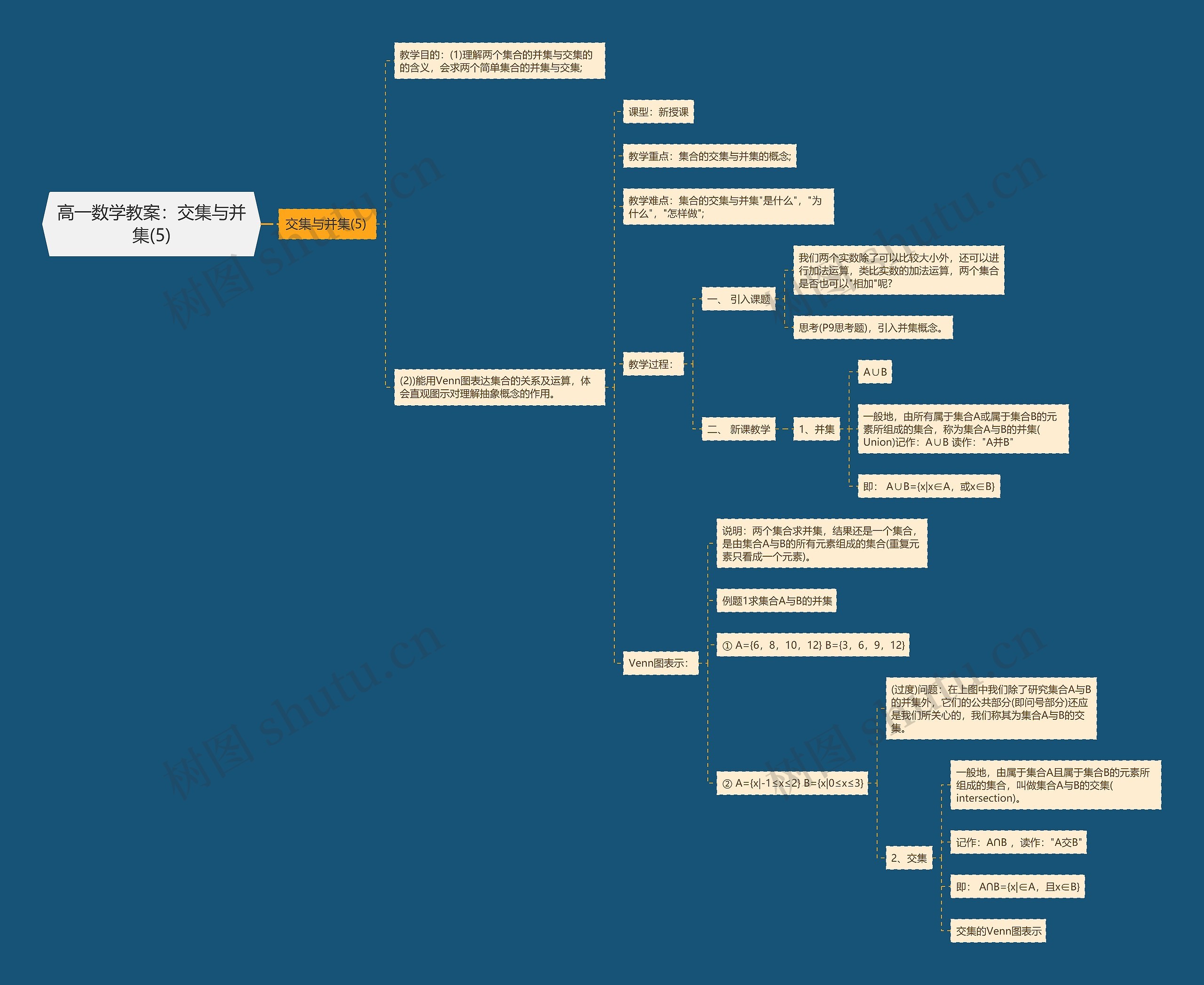
交集与并集(5)
教学目的：(1)理解两个集合的并集与交集的的含义，会求两个简单集合的并集与交集;
(2))能用Venn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用。
课型：新授课
教学重点：集合的交集与并集的概念;
教学难点：集合的交集与并集"是什么"，"为什么"，"怎样做";
教学过程：
一、 引入课题
我们两个实数除了可以比较大小外，还可以进行加法运算，类比实数的加法运算，两个集合是否也可以"相加"呢?
思考(P9思考题)，引入并集概念。
二、 新课教学
1、并集
A∪B
一般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集(Union)记作：A∪B 读作："A并B"
即： A∪B={x|x∈A，或x∈B}
Venn图表示：
说明：两个集合求并集，结果还是一个集合，是由集合A与B的所有元素组成的集合(重复元素只看成一个元素)。
例题1求集合A与B的并集
① A={6，8，10，12} B={3，6，9，12}
② A={x|-1≤x≤2} B={x|0≤x≤3}
(过度)问题：在上图中我们除了研究集合A与B的并集外，它们的公共部分(即问号部分)还应是我们所关心的，我们称其为集合A与B的交集。
2、交集
一般地，由属于集合A且属于集合B的元素所组成的集合，叫做集合A与B的交集(intersection)。
记作：A∩B ，读作："A交B"
即： A∩B={x|∈A，且x∈B}
交集的Venn图表示
相关思维导图模板
树图思维导图提供 高一数学教案：交集与并集(3) 在线思维导图免费制作，点击“编辑”按钮，可对 高一数学教案：交集与并集(3) 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a7a6e9e02606592756d57772b1736b93
树图思维导图提供 高一数学教案：交集与并集(2) 在线思维导图免费制作，点击“编辑”按钮，可对 高一数学教案：交集与并集(2) 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7d4ac02dd508fa3d6ac55bb657f71899
沪公网安备 31011502019485号
上海工商