笔灵AI论文写作三步搞定，GO>>
高二数学复习方法：平方差公式汇总思维导图
会员免费下载或30积分
会员免费使用或30积分
深拥意中人 浏览量：252023-04-20 17:09:40
已被使用0次
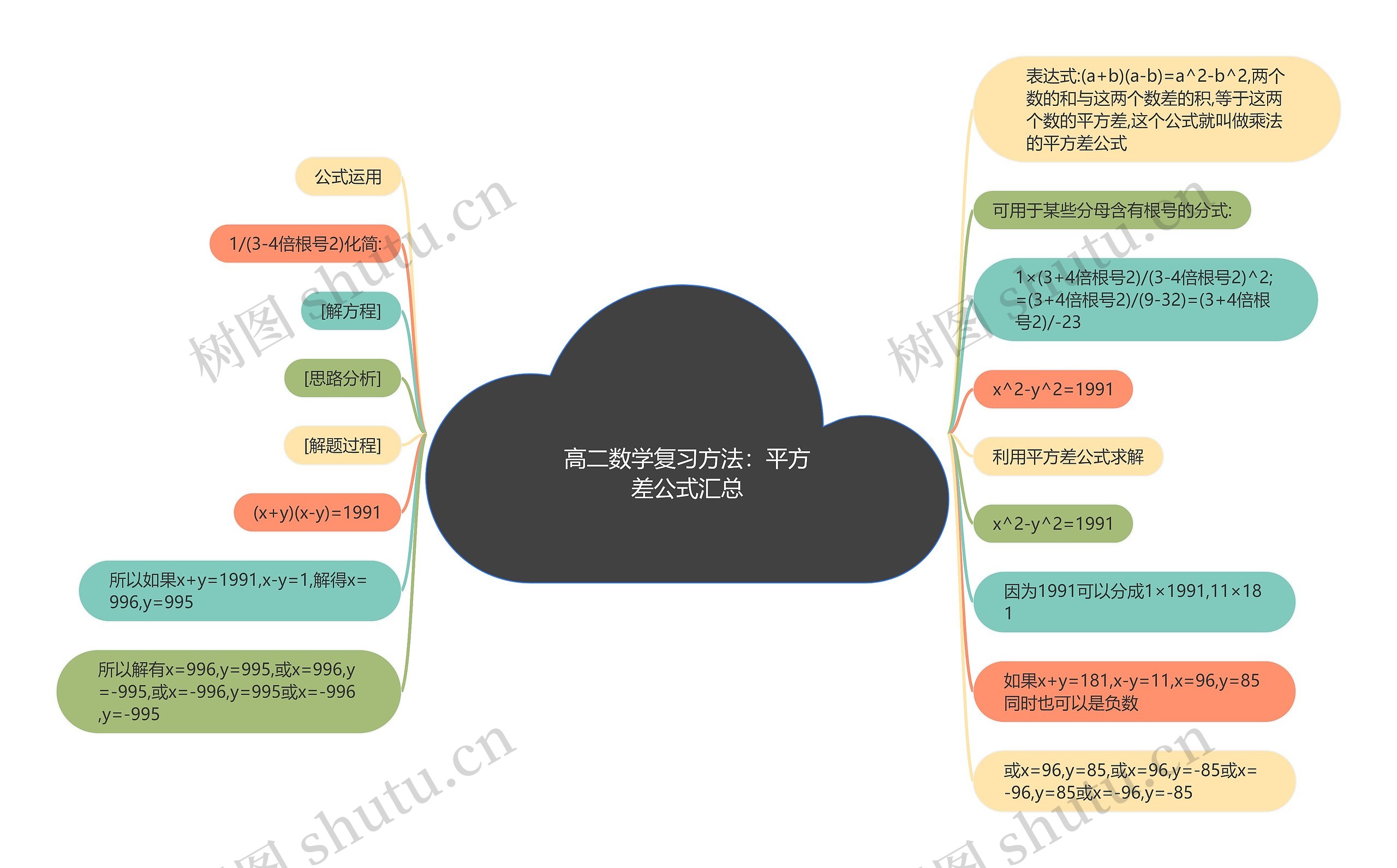
高二数学复习方法：平方差公式汇总思维导图平方差公式表达式为(a+b)(a-b)=a^2-b^2，表示两个数的和与这两个数差的积等于他的平方差。这个公式在解决一些分母含有根号的分式时非常有用，在化简1/(3-4倍根号2)时，可以使用乘法的平方差公式来化简得到(3+4倍根号2)/-23。在解方程时，利用平方差公式可以帮助我们求解。对于方程x^2-y^2=1991，可以利用平方差公式将其转化为(x+y)(x-y)=1991，通过分解1991，可以得到多组解，如x=996，y=995或x=996，y=-995，还可以取x=96，y=85等，同时也可以是负数，平方差公式是高二数学复习中不可或缺的知识点。
思维导图大纲
高二数学复习方法：平方差公式汇总思维导图模板大纲
表达式:(a+b)(a-b)=a^2-b^2,两个数的和与这两个数差的积,等于这两个数的平方差,这个公式就叫做乘法的平方差公式
公式运用
可用于某些分母含有根号的分式:
1/(3-4倍根号2)化简:
1×(3+4倍根号2)/(3-4倍根号2)^2;=(3+4倍根号2)/(9-32)=(3+4倍根号2)/-23
[解方程]
x^2-y^2=1991
[思路分析]
利用平方差公式求解
[解题过程]
x^2-y^2=1991
(x+y)(x-y)=1991
因为1991可以分成1×1991,11×181
所以如果x+y=1991,x-y=1,解得x=996,y=995
如果x+y=181,x-y=11,x=96,y=85同时也可以是负数
所以解有x=996,y=995,或x=996,y=-995,或x=-996,y=995或x=-996,y=-995
或x=96,y=85,或x=96,y=-85或x=-96,y=85或x=-96,y=-85
沪公网安备 31011502019485号
上海工商