考研《高等数学》复习思维导图
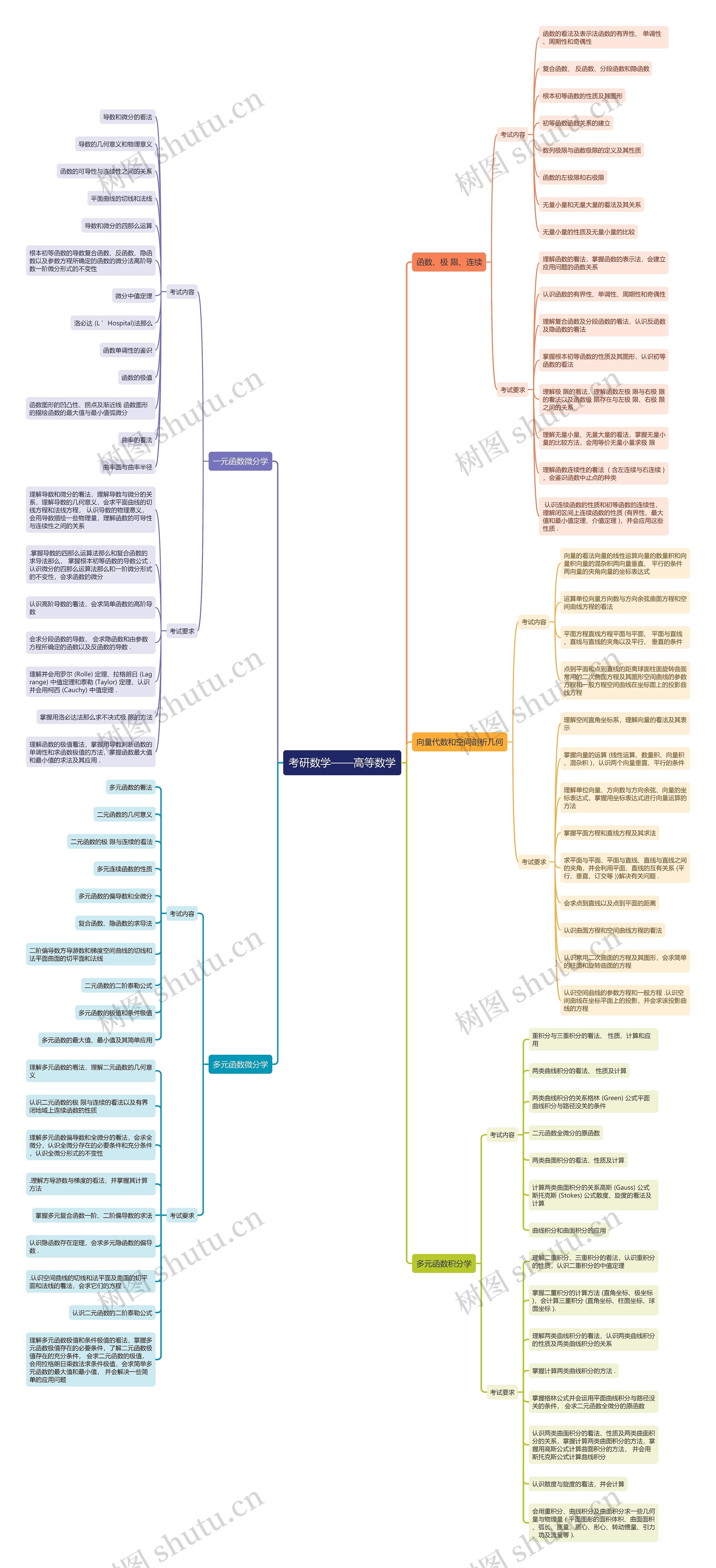
考研《高等数学》复习思维导图中包含了函数、极限、连续等内容,考试要求理解函数的看法和表示法,掌握函数的性质和初等函数的图形,和复合函数、反函数、分段函数和隐函数的性质和求法,还需要了解数列极限和函数极限的定义性质,和无量小量和无量大量的看法关系和比较。还需要理解函数的连续性,包含左极限和右极限,和闭区间上连续函数的性质。在微分学方面,需要掌握导数和微分的看法和运算,能够判断函数的单调性和求函数的极值,和了解曲率、曲率圆和曲率半径的看法,在向量代数和空间解析几何中,需要理解向量的看法线性运算、数量积和向量积。并掌握平面方程和直线方程的求法,和空间曲线和曲面的方程和投影,在多元函数积分学方面,需要理解二重积分和三重积分的看法和计算方法,和曲线积分和曲面积分的性质和计算方法,还需要能够运用相关公式求一些几何量和物理量。
思维导图大纲
考研数学——高等数学思维导图模板大纲
函数、极 限、连续
考试内容
函数的看法及表示法函数的有界性、 单调性、周期性和奇偶性
复合函数、 反函数、分段函数和隐函数
根本初等函数的性质及其图形
初等函数函数关系的建立
数列极限与函数极限的定义及其性质
函数的左极限和右极限
无量小量和无量大量的看法及其关系
无量小量的性质及无量小量的比较
考试要求
理解函数的看法,掌握函数的表示法,会建立应用问题的函数关系
认识函数的有界性、单调性、周期性和奇偶性
理解复合函数及分段函数的看法,认识反函数及隐函数的看法
掌握根本初等函数的性质及其图形,认识初等函数的看法
理解极 限的看法,理解函数左极 限与右极 限的看法以及函数极 限存在与左极 限、右极 限之间的关系
理解无量小量、无量大量的看法,掌握无量小量的比较方法,会用等价无量小量求极 限
理解函数连续性的看法 ( 含左连续与右连续 ),会鉴识函数中止点的种类
认识连续函数的性质和初等函数的连续性, 理解闭区间上连续函数的性质 (有界性、最大值和最小值定理、介值定理 ),并会应用这些性质 .
一元函数微分学
考试内容
导数和微分的看法
导数的几何意义和物理意义
函数的可导性与连续性之间的关系
平面曲线的切线和法线
导数和微分的四那么运算
根本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性
微分中值定理
洛必达 (L ’Hospital)法那么
函数单调性的鉴识
函数的极值
函数图形的凹凸性、拐点及渐近线 函数图形的描绘函数的最大值与最小值弧微分
曲率的看法
曲率圆与曲率半径
考试要求
理解导数和微分的看法,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程, 认识导数的物理意义, 会用导数描绘一些物理量,理解函数的可导性与连续性之间的关系
.掌握导数的四那么运算法那么和复合函数的求导法那么, 掌握根本初等函数的导数公式 .认识微分的四那么运算法那么和一阶微分形式的不变性,会求函数的微分
认识高阶导数的看法,会求简单函数的高阶导数
会求分段函数的导数, 会求隐函数和由参数方程所确定的函数以及反函数的导数 .
理解并会用罗尔 (Rolle) 定理、拉格朗日 (Lagrange) 中值定理和泰勒 (Taylor) 定理,认识并会用柯西 (Cauchy) 中值定理 .
掌握用洛必达法那么求不决式极 限的方法
理解函数的极值看法,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用 .
多元函数微分学
考试内容
多元函数的看法
二元函数的几何意义
二元函数的极 限与连续的看法
多元连续函数的性质
多元函数的偏导数和全微分
复合函数、隐函数的求导法
二阶偏导数方导游数和梯度空间曲线的切线和法平面曲面的切平面和法线
二元函数的二阶泰勒公式
多元函数的极值和条件极值
多元函数的最大值、最小值及其简单应用
考试要求
理解多元函数的看法,理解二元函数的几何意义
认识二元函数的极 限与连续的看法以及有界闭地域上连续函数的性质
理解多元函数偏导数和全微分的看法,会求全微分,认识全微分存在的必要条件和充分条件,认识全微分形式的不变性
.理解方导游数与梯度的看法,并掌握其计算方法
掌握多元复合函数一阶、二阶偏导数的求法
认识隐函数存在定理,会求多元隐函数的偏导数 .
.认识空间曲线的切线和法平面及曲面的切平面和法线的看法,会求它们的方程 .
认识二元函数的二阶泰勒公式
理解多元函数极值和条件极值的看法,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件, 会求二元函数的极值, 会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值, 并会解决一些简单的应用问题
向量代数和空间剖析几何
考试内容
向量的看法向量的线性运算向量的数量积和向量积向量的混杂积两向量垂直、 平行的条件两向量的夹角向量的坐标表达式
运算单位向量方向数与方向余弦曲面方程和空间曲线方程的看法
平面方程直线方程平面与平面、 平面与直线、直线与直线的夹角以及平行、 垂直的条件
点到平面和点到直线的距离球面柱面旋转曲面常用的二次曲面方程及其图形空间曲线的参数方程和一般方程空间曲线在坐标面上的投影曲线方程
考试要求
理解空间直角坐标系,理解向量的看法及其表示
掌握向量的运算 (线性运算、数量积、向量积、混杂积 ),认识两个向量垂直、平行的条件
理解单位向量、方向数与方向余弦、向量的坐标表达式,掌握用坐标表达式进行向量运算的方法
掌握平面方程和直线方程及其求法
求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的互有关系 (平行、垂直、订交等 ))解决有关问题 .
会求点到直线以及点到平面的距离
认识曲面方程和空间曲线方程的看法
认识常用二次曲面的方程及其图形,会求简单的柱面和旋转曲面的方程
认识空间曲线的参数方程和一般方程 .认识空间曲线在坐标平面上的投影,并会求该投影曲线的方程
多元函数积分学
考试内容
重积分与三重积分的看法、 性质、计算和应用
两类曲线积分的看法、 性质及计算
两类曲线积分的关系格林 (Green) 公式平面曲线积分与路径没关的条件
二元函数全微分的原函数
两类曲面积分的看法、性质及计算
计算两类曲面积分的关系高斯 (Gauss) 公式斯托克斯 (Stokes) 公式散度、旋度的看法及计算
曲线积分和曲面积分的应用
考试要求
理解二重积分、三重积分的看法,认识重积分的性质,认识二重积分的中值定理
掌握二重积分的计算方法 (直角坐标、极坐标 ),会计算三重积分 (直角坐标、柱面坐标、球面坐标 ).
理解两类曲线积分的看法,认识两类曲线积分的性质及两类曲线积分的关系
掌握计算两类曲线积分的方法 .
掌握格林公式并会运用平面曲线积分与路径没关的条件, 会求二元函数全微分的原函数
认识两类曲面积分的看法、性质及两类曲面积分的关系,掌握计算两类曲面积分的方法,掌握用高斯公式计算曲面积分的方法, 并会用斯托克斯公式计算曲线积分
认识散度与旋度的看法,并会计算
会用重积分、曲线积分及曲面积分求一些几何量与物理量 ( 平面图形的面积体积、曲面面积、弧长、质量、质心、形心、转动惯量、引力、功及流量等 ).
相关思维导图模板


树图思维导图提供 高等数学知识点 在线思维导图免费制作,点击“编辑”按钮,可对 高等数学知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9b4c755584cd33ead3f894e2eb35a493
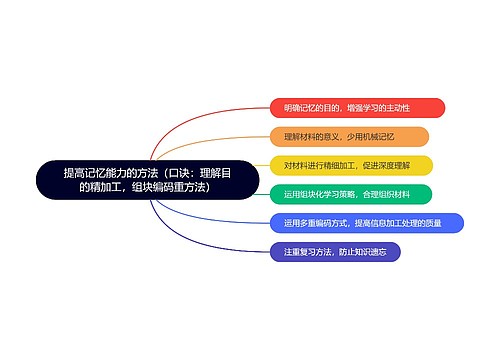

树图思维导图提供 提高记忆能力的方法 (口诀:理解目的精加工,组块编码重方法) 在线思维导图免费制作,点击“编辑”按钮,可对 提高记忆能力的方法 (口诀:理解目的精加工,组块编码重方法) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:75af1bfbe3db7416de1aa27196d0086b










 上海工商
上海工商