高中物理力的应用方法思维导图
物体的受力情况不同,物体可处于不同的运动状态,要研究物体的运动,必须分析物体的受力情况,正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本功。这次小编给大家整理了高中物理力的应用方法知识点思维导图,供大家阅读参考。
树图思维导图提供 高中物理力的应用方法思维导图 在线思维导图免费制作,点击“编辑”按钮,可对 高中物理力的应用方法思维导图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:47944c0f787638200789f16be0d2a360
思维导图大纲
高中物理力的应用方法知识点思维导图模板大纲
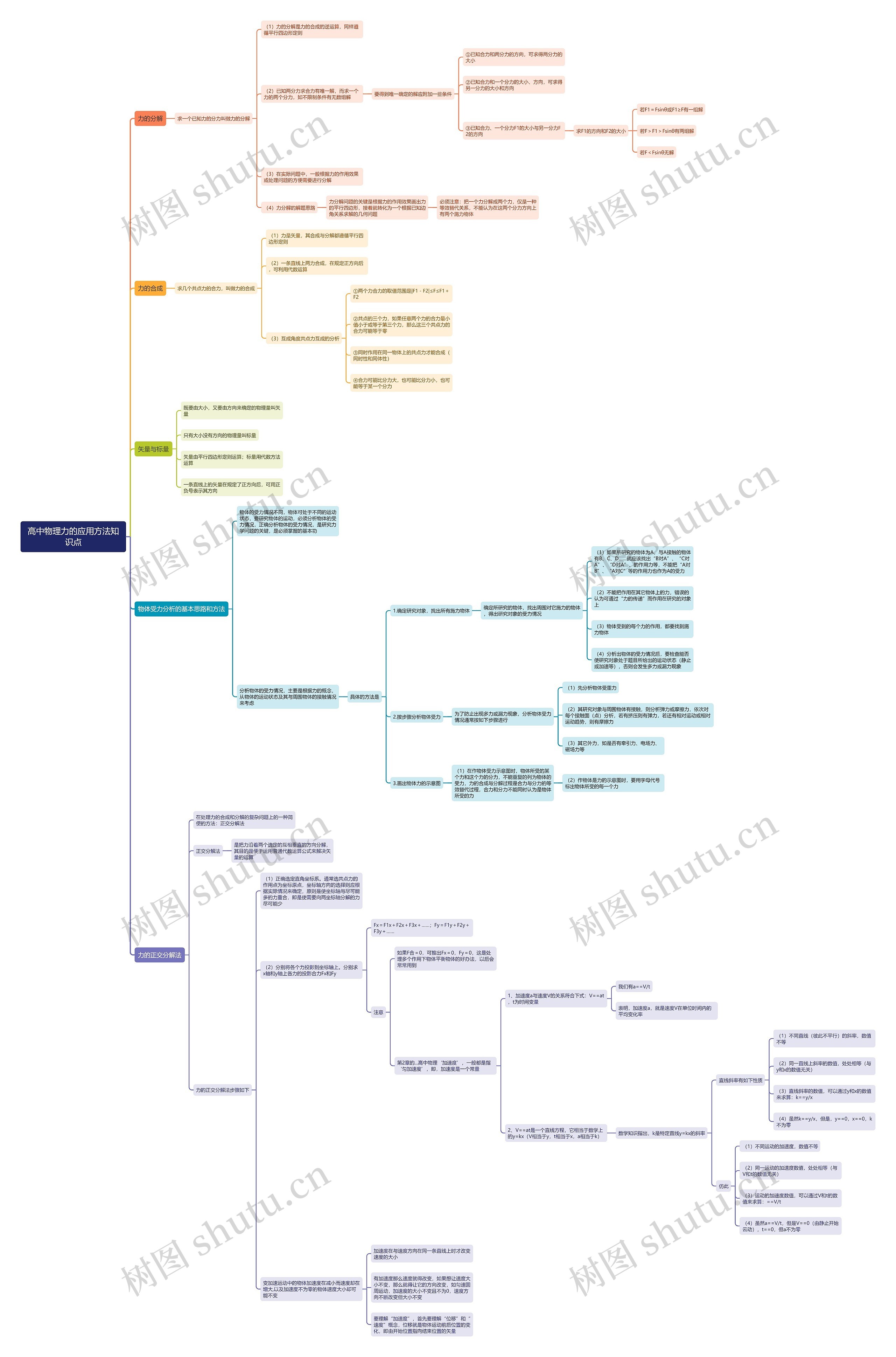
力的分解
求一个已知力的分力叫做力的分解
(1)力的分解是力的合成的逆运算,同样遵循平行四边形定则
(2)已知两分力求合力有唯一解,而求一个力的两个分力,如不限制条件有无数组解
要得到唯一确定的解应附加一些条件
①已知合力和两分力的方向,可求得两分力的大小
②已知合力和一个分力的大小、方向,可求得另一分力的大小和方向
③已知合力、一个分力F1的大小与另一分力F2的方向
求F1的方向和F2的大小
若F1=Fsinθ或F1≥F有一组解
若F>F1>Fsinθ有两组解
若F<Fsinθ无解
(3)在实际问题中,一般根据力的作用效果或处理问题的方便需要进行分解
(4)力分解的解题思路
力分解问题的关键是根据力的作用效果画出力的平行四边形,接着就转化为一个根据已知边角关系求解的几何问题
必须注意:把一个力分解成两个力,仅是一种等效替代关系,不能认为在这两个分力方向上有两个施力物体
力的合成
求几个共点力的合力,叫做力的合成
(1)力是矢量,其合成与分解都遵循平行四边形定则
(2)一条直线上两力合成,在规定正方向后,可利用代数运算
(3)互成角度共点力互成的分析
①两个力合力的取值范围是|F1-F2|≤F≤F1+F2
②共点的三个力,如果任意两个力的合力最小值小于或等于第三个力,那么这三个共点力的合力可能等于零
③同时作用在同一物体上的共点力才能合成(同时性和同体性)
④合力可能比分力大,也可能比分力小,也可能等于某一个分力
矢量与标量
既要由大小,又要由方向来确定的物理量叫矢量
只有大小没有方向的物理量叫标量
矢量由平行四边形定则运算;标量用代数方法运算
一条直线上的矢量在规定了正方向后,可用正负号表示其方向
物体受力分析的基本思路和方法
物体的受力情况不同,物体可处于不同的运动状态,要研究物体的运动,必须分析物体的受力情况,正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本功
分析物体的受力情况,主要是根据力的概念,从物体的运动状态及其与周围物体的接触情况来考虑
具体的方法是
1.确定研究对象,找出所有施力物体
确定所研究的物体,找出周围对它施力的物体,得出研究对象的受力情况
(1)如果所研究的物体为A,与A接触的物体有B、C、D……就应该找出“B对A”、“C对A”、“D对A”、的作用力等,不能把“A对B”、“A对C”等的作用力也作为A的受力
(2)不能把作用在其它物体上的力,错误的认为可通过“力的传递”而作用在研究的对象上
(3)物体受到的每个力的作用,都要找到施力物体
(4)分析出物体的受力情况后,要检查能否使研究对象处于题目所给出的运动状态(静止或加速等),否则会发生多力或漏力现象
2.按步骤分析物体受力
为了防止出现多力或漏力现象,分析物体受力情况通常按如下步骤进行
(1)先分析物体受重力
(2)其研究对象与周围物体有接触,则分析弹力或摩擦力,依次对每个接触面(点)分析,若有挤压则有弹力,若还有相对运动或相对运动趋势,则有摩擦力
(3)其它外力,如是否有牵引力、电场力、磁场力等
3.画出物体力的示意图
(1)在作物体受力示意图时,物体所受的某个力和这个力的分力,不能重复的列为物体的受力,力的合成与分解过程是合力与分力的等效替代过程,合力和分力不能同时认为是物体所受的力
(2)作物体是力的示意图时,要用字母代号标出物体所受的每一个力
力的正交分解法
在处理力的合成和分解的复杂问题上的一种简便的方法:正交分解法
正交分解法
是把力沿着两个选定的互相垂直的方向分解,其目的是便于运用普通代数运算公式来解决矢量的运算
力的正交分解法步骤如下
(1)正确选定直角坐标系。通常选共点力的作用点为坐标原点,坐标轴方向的选择则应根据实际情况来确定,原则是使坐标轴与尽可能多的力重合,即是使需要向两坐标轴分解的力尽可能少
(2)分别将各个力投影到坐标轴上。分别求x轴和y轴上各力的投影合力Fx和Fy
Fx=F1x+F2x+F3x+……;Fy=F1y+F2y+F3y+……
注意
如果F合=0,可推出Fx=0,Fy=0,这是处理多个作用下物体平衡物体的好办法,以后会常常用到
第2章的...高中物理‘加速度’,一般都是指‘匀加速度’,即,加速度是一个常量
1、加速度a与速度V的关系符合下式:V==at,t为时间变量
我们有a==V/t
表明,加速度a,就是速度V在单位时间内的平均变化率
2、V==at是一个直线方程,它相当于数学上的y=kx(V相当于y,t相当于x,a相当于k)
数学知识指出,k是特定直线y=kx的斜率
直线斜率有如下性质
(1)不同直线(彼此不平行)的斜率,数值不等
(2)同一直线上斜率的数值,处处相等(与y和x的数值无关)
(3)直线斜率的数值,可以通过y和x的数值来求算:k==y/x
(4)虽然k==y/x,但是,y==0,x==0,k不为零
仿此
(1)不同运动的加速度,数值不等
(2)同一运动的加速度数值,处处相等(与V和t的数值无关)
(3)运动的加速度数值,可以通过V和t的数值来求算:==V/t
(4)虽然a==V/t,但是V==0(由静止开始云动),t==0,但a不为零
变加速运动中的物体加速度在减小而速度却在增大,以及加速度不为零的物体速度大小却可能不变
加速度在与速度方向在同一条直线上时才改变速度的大小
有加速度那么速度就得改变,如果想让速度大小不变,那么就得让它的方向改变,如匀速圆周运动,加速度的大小不变且不为0,速度方向不断改变但大小不变
要理解“加速度”,首先要理解“位移”和“速度”概念,位移就是物体运动前后位置的变化,即由开始位置指向结束位置的矢量
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 销售经理半年规划 在线思维导图免费制作,点击“编辑”按钮,可对 销售经理半年规划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:e614d6bcf03e9318109240a18697c5d1













 上海工商
上海工商