对于三年级学生寒假数学辅导之应用题的注意事项思维导图
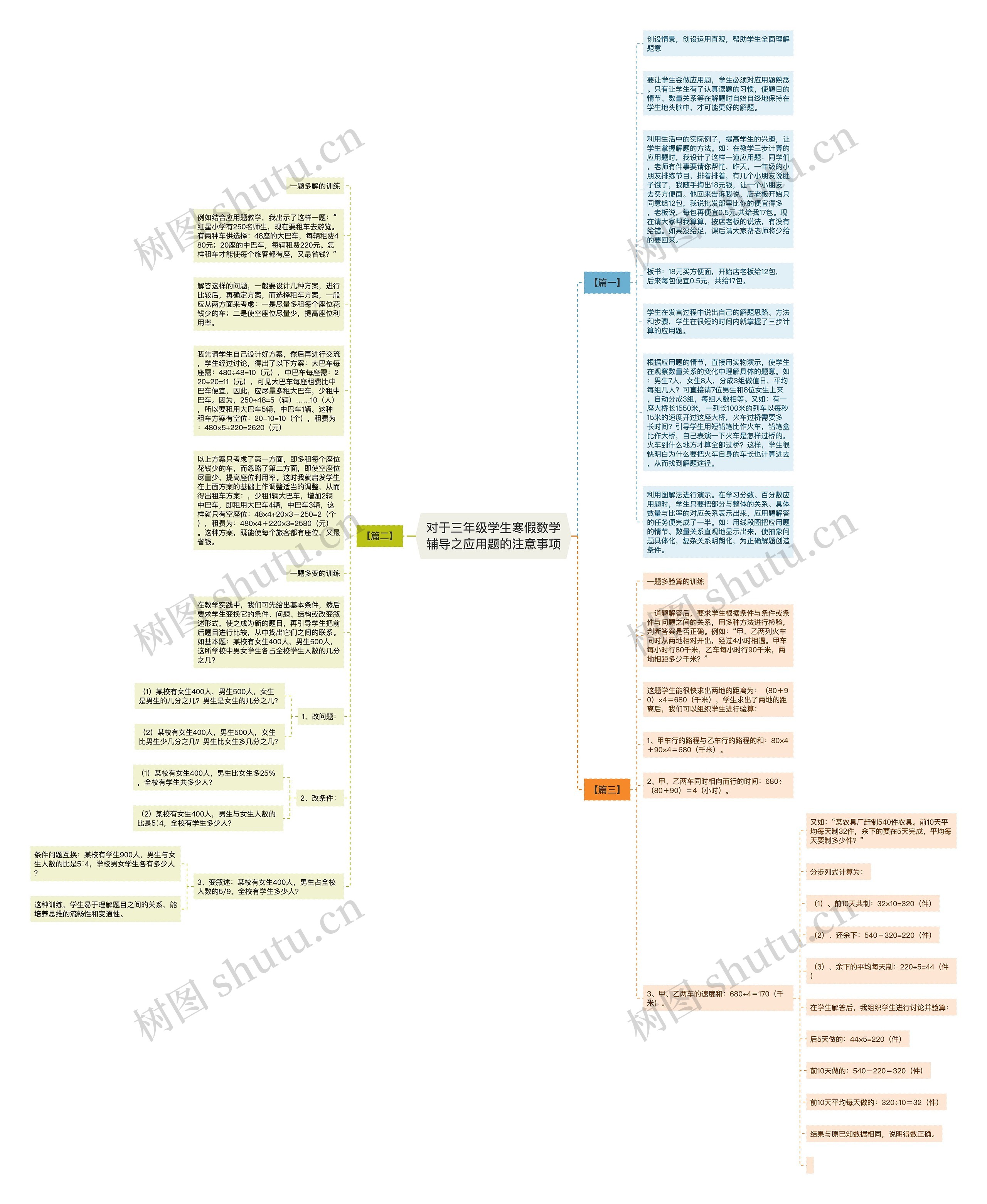
对于三年级学生寒假数学辅导之应用题的注意事项思维导图包含以下知识点:创设生动的情景,运用直观示例帮助学生理解题意。利用“一题多解”的方法,鼓励学生自己尝试解题,并进行交流,提高学生的解题能力,对于分数、百分数应用题,可以利用图解法进行演示,使学生直观地理解题目的情节和数量关系。通过实物演示,让学生通过观察数量关系的变化来更好的理解题目,一定要让学生养成认真读题的习惯,使题目的情节、数量关系在解题时能够自始至终地保持在学生的脑海中,才可能更好的解决问题。
思维导图大纲
对于三年级学生寒假数学辅导之应用题的注意事项思维导图模板大纲
【篇一】
创设情景,创设运用直观,帮助学生全面理解题意
要让学生会做应用题,学生必须对应用题熟悉。只有让学生有了认真读题的习惯,使题目的情节、数量关系等在解题时自始自终地保持在学生地头脑中,才可能更好的解题。
利用生活中的实际例子,提高学生的兴趣,让学生掌握解题的方法。如:在教学三步计算的应用题时,我设计了这样一道应用题:同学们,老师有件事要请你帮忙,昨天,一年级的小朋友排练节目,排着排着,有几个小朋友说肚子饿了,我随手掏出18元钱,让一个小朋友去买方便面。他回来告诉我说,店老板开始只同意给12包,我说批发部里比你的便宜得多,老板说,每包再便宜0.5元,共给我17包。现在请大家帮我算算,按店老板的说法,有没有给错。如果没给足,课后请大家帮老师将少给的要回来。
板书:18元买方便面,开始店老板给12包,后来每包便宜0.5元,共给17包。
学生在发言过程中说出自己的解题思路、方法和步骤,学生在很短的时间内就掌握了三步计算的应用题。
根据应用题的情节,直接用实物演示,使学生在观察数量关系的变化中理解具体的题意。如:男生7人,女生8人,分成3组做值日,平均每组几人?可直接请7位男生和8位女生上来,自动分成3组,每组人数相等。又如:有一座大桥长1550米,一列长100米的列车以每秒15米的速度开过这座大桥,火车过桥需要多长时间?引导学生用短铅笔比作火车,铅笔盒比作大桥,自己表演一下火车是怎样过桥的。火车到什么地方才算全部过桥?这样,学生很快明白为什么要把火车自身的车长也计算进去,从而找到解题途径。
利用图解法进行演示。在学习分数、百分数应用题时,学生只要把部分与整体的关系、具体数量与比率的对应关系表示出来,应用题解答的任务便完成了一半。如:用线段图把应用题的情节、数量关系直观地显示出来,使抽象问题具体化,复杂关系明朗化,为正确解题创造条件。
【篇二】
一题多解的训练
例如结合应用题教学,我出示了这样一题:“红星小学有250名师生,现在要租车去游览。有两种车供选择:48座的大巴车,每辆租费480元;20座的中巴车,每辆租费220元。怎样租车才能使每个旅客都有座,又最省钱?”
解答这样的问题,一般要设计几种方案,进行比较后,再确定方案,而选择租车方案,一般应从两方面来考虑:一是尽量多租每个座位花钱少的车;二是使空座位尽量少,提高座位利用率。
我先请学生自己设计好方案,然后再进行交流,学生经过讨论,得出了以下方案:大巴车每座需:480÷48=10(元),中巴车每座需:220÷20=11(元),可见大巴车每座租费比中巴车便宜,因此,应尽量多租大巴车,少租中巴车。因为,250÷48=5(辆)……10(人),所以要租用大巴车5辆,中巴车1辆。这种租车方案有空位:20-10=10(个),租费为:480×5+220=2620(元)
以上方案只考虑了第一方面,即多租每个座位花钱少的车,而忽略了第二方面,即使空座位尽量少,提高座位利用率。这时我就启发学生在上面方案的基础上作调整适当的调整,从而得出租车方案:,少租1辆大巴车,增加2辆中巴车,即租用大巴车4辆,中巴车3辆,这样就只有空座位:48×4+20×3-250=2(个),租费为:480×4+220×3=2580(元)。这种方案,既能使每个旅客都有座位,又最省钱。
一题多变的训练
在教学实践中,我们可先给出基本条件,然后要求学生变换它的条件、问题、结构或改变叙述形式,使之成为新的题目,再引导学生把前后题目进行比较,从中找出它们之间的联系。如基本题:某校有女生400人,男生500人,这所学校中男女学生各占全校学生人数的几分之几?
1、改问题:
(1)某校有女生400人,男生500人,女生是男生的几分之几?男生是女生的几分之几?
(2)某校有女生400人,男生500人,女生比男生少几分之几?男生比女生多几分之几?
2、改条件:
(1)某校有女生400人,男生比女生多25%,全校有学生共多少人?
(2)某校有女生400人,男生与女生人数的比是5∶4,全校有学生多少人?
3、变叙述:某校有女生400人,男生占全校人数的5/9,全校有学生多少人?
条件问题互换:某校有学生900人,男生与女生人数的比是5∶4,学校男女学生各有多少人?
这种训练,学生易于理解题目之间的关系,能培养思维的流畅性和变通性。
【篇三】
一题多验算的训练
一道题解答后,要求学生根据条件与条件或条件与问题之间的关系,用多种方法进行检验,判断答案是否正确。例如:“甲、乙两列火车同时从两地相对开出,经过4小时相遇。甲车每小时行80千米,乙车每小时行90千米,两地相距多少千米?”
这题学生能很快求出两地的距离为:(80+90)×4=680(千米),学生求出了两地的距离后,我们可以组织学生进行验算:
1、甲车行的路程与乙车行的路程的和:80×4+90×4=680(千米)。
2、甲、乙两车同时相向而行的时间:680÷(80+90)=4(小时)。
3、甲、乙两车的速度和:680÷4=170(千米)。
又如:“某农具厂赶制540件农具。前10天平均每天制32件,余下的要在5天完成,平均每天要制多少件?”
分步列式计算为:
(1)、前10天共制:32×10=320(件)
(2)、还余下:540-320=220(件)
(3)、余下的平均每天制:220÷5=44(件)
在学生解答后,我组织学生进行讨论并验算:
后5天做的:44×5=220(件)
前10天做的:540-220=320(件)
前10天平均每天做的:320÷10=32(件)
结果与原已知数据相同,说明得数正确。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a









 上海工商
上海工商