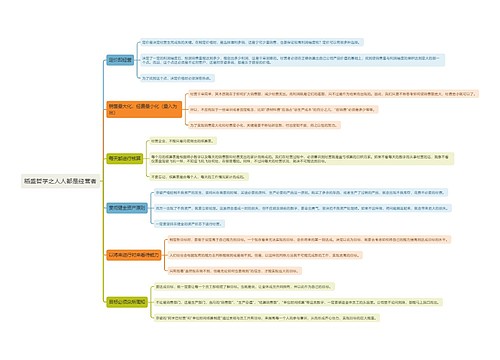
2022国考数量关系干货分享之相遇问题思维导图

相遇问题是数量关系中一类较为常考的题型,同样也是技巧性较强的题型。虽然相遇问题看似类型较为复杂,分成多种情况,但实际上本质就是找到问题的核心所在。考查考生的逻辑思维能力,通过使用特殊的技巧解决相遇问题。
树图思维导图提供 2022国考数量关系干货分享之相遇问题 在线思维导图免费制作,点击“编辑”按钮,可对 2022国考数量关系干货分享之相遇问题 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:8f671176fa176bf5a8c17e6f12202759
思维导图大纲
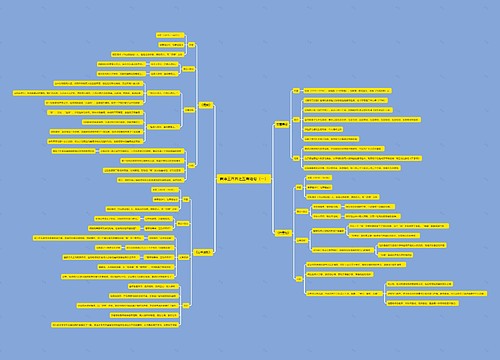
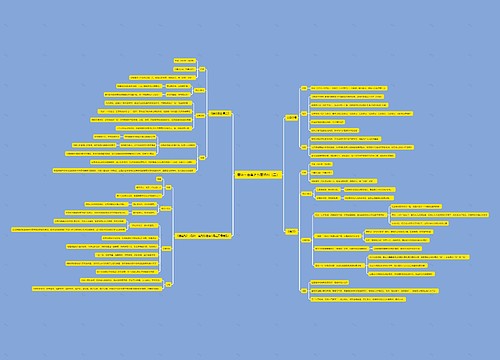
2022国考数量关系干货分享之相遇问题思维导图模板大纲
相遇问题是数量关系中一类较为常考的题型,同样也是技巧性较强的题型。虽然相遇问题看似类型较为复杂,分成多种情况,但实际上本质就是找到问题的核心所在。考查考生的逻辑思维能力,通过使用特殊的技巧解决相遇问题。下面就相遇问题的题型进行具体分析:
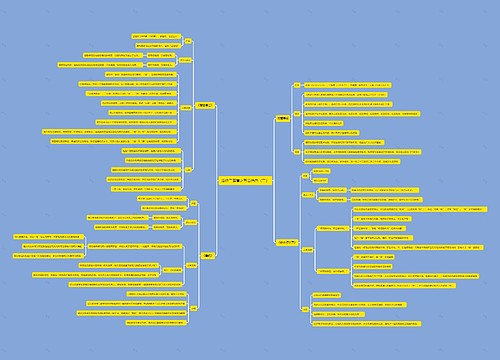
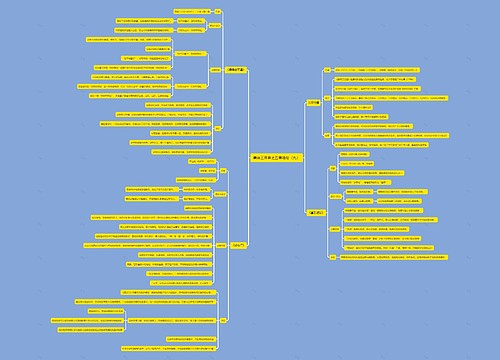
一、单次相遇问题
在相遇问题中,凡是方向相反的都可以看成相遇问题。引用公式。
【例1】甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问AB两地的距离为多少米?
A. 8000米
B. 8500米
C. 10000米
D. 10500米
【解析】第一步,本题考查行程问题,属于相遇追及类,用方程法解题。
第二步,设AB两地的距离为S,甲丙相遇时间为t,由甲丙相遇可得:S=(85+65)脳t①;由甲丙相遇5分钟后乙丙相遇可得:S=(75+65)脳(t+5)②。联立①②,解得S=10500米。
因此,选择D选项。
在这道题中,核心在于无论甲乙相遇还是乙丙相遇,走的路程总和都为AB两地之间的距离,这就是典型的相遇问题中直线型单次相遇,直接代入公式即可。
二、多次相遇问题
在多次相遇问题中,要先识别是属于两端出发还是单端出发问题,再代入公式,直线型两端出发n次相遇:(2n-1)S=()脳t;以及直线型单端出发n次相遇:2nS=()脳t。
【例二】在一次航海模型展示活动中,甲乙两款模型在长100米的水池两边同时开始相向匀速航行,甲款模型航行100米要72秒,乙款模型航行100米要60秒,若调头转身时间略去不计,在12分钟内甲乙两款模型相遇次数是:
A. 9
B. 10
C. 11
D. 12
【解析】第一步,本题考查行程问题,属于相遇追及类。
第二步,12分钟=720秒。设共相遇n次,则总共行驶距离S=(2n-1)S,利用两端出发多次相遇问题公式(2n-1)S=()脳t,可得(2n-1)脳100=()脳720。
第三步,解得n=11.5,故迎面相遇11次。
因此,选择C选项。
在这道题中,问题的核心在于看出这是单端还是两端出发,甲乙两款模型从两边开始航行,证明是两端出发问题,因此,引用公式(2n-1)S=()脳t。
三、环型相遇问题
在环型问题中,在同一起点出发,要先识别方向是同向还是异向相遇,同向出发证明速度快的比速度慢的多跑了一圈,再代入公式即可,同向:S=()脳t;以及异向:S=()脳t。
【例三】甲、乙两人在一条400米的环形跑道上从相距200米的位置出发,同向匀速跑步。当甲第三次追上乙的时候,乙跑了2000米。问甲的速度是乙的多少倍?
A. 1.2
B. 1.5
C. 1.6
D. 2.0
【解析】第一步,本题考查行程问题,属于相遇追及类。
第二步,环形同点同向出发每追上一次,甲比乙多跑一圈。第一次由于是不同起点,甲比乙多跑原来的差距200米;之后两次追上都多跑400米,甲一共比乙多跑200+400脳2=1000(米)。乙跑了2000米,甲跑了3000米,时间相同,则速度比与路程比也相同,可知甲的速度是乙的3000梅2000=1.5倍。
因此,选择B选项。
在这道题中,因为同向出发,所以代入公式S=()脳t,又因为起点不同,起点相距200米,因此第一次甲比乙多走200米,就能够通过乙的路程算出甲所走的全程。





 上海工商
上海工商