国考行测数量关系之秒设未知数,快解应用题思维导图
历年国省考行测数量关系中必有几道基础应用题,部分题目可利用赋值法、数字特性法等精妙方法快速解题,但也有部分题目只能追根溯源通过设未知数、找等量关系、建立方程(组)求解得出答案。
树图思维导图提供 国考行测数量关系之秒设未知数,快解应用题 在线思维导图免费制作,点击“编辑”按钮,可对 国考行测数量关系之秒设未知数,快解应用题 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5d125eb549e8bd9a7b7ae24b058354b3
思维导图大纲
国考行测数量关系之秒设未知数,快解应用题思维导图模板大纲
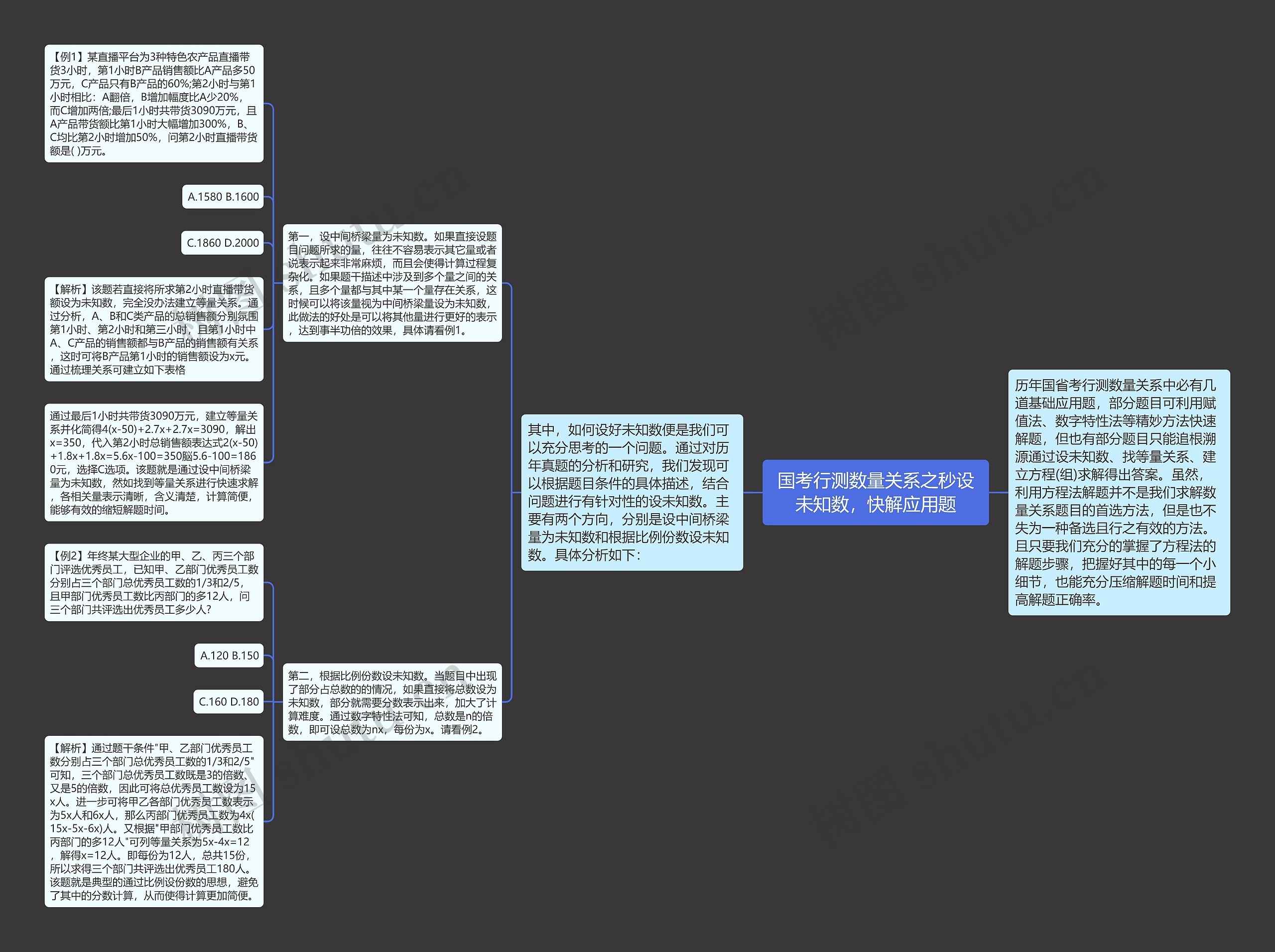
历年国省考行测数量关系中必有几道基础应用题,部分题目可利用赋值法、数字特性法等精妙方法快速解题,但也有部分题目只能追根溯源通过设未知数、找等量关系、建立方程(组)求解得出答案。虽然,利用方程法解题并不是我们求解数量关系题目的首选方法,但是也不失为一种备选且行之有效的方法。且只要我们充分的掌握了方程法的解题步骤,把握好其中的每一个小细节,也能充分压缩解题时间和提高解题正确率。
其中,如何设好未知数便是我们可以充分思考的一个问题。通过对历年真题的分析和研究,我们发现可以根据题目条件的具体描述,结合问题进行有针对性的设未知数。主要有两个方向,分别是设中间桥梁量为未知数和根据比例份数设未知数。具体分析如下:
第一,设中间桥梁量为未知数。如果直接设题目问题所求的量,往往不容易表示其它量或者说表示起来非常麻烦,而且会使得计算过程复杂化。如果题干描述中涉及到多个量之间的关系,且多个量都与其中某一个量存在关系,这时候可以将该量视为中间桥梁量设为未知数,此做法的好处是可以将其他量进行更好的表示,达到事半功倍的效果,具体请看例1。
【例1】某直播平台为3种特色农产品直播带货3小时,第1小时B产品销售额比A产品多50万元,C产品只有B产品的60%;第2小时与第1小时相比:A翻倍,B增加幅度比A少20%,而C增加两倍;最后1小时共带货3090万元,且A产品带货额比第1小时大幅增加300%,B、C均比第2小时增加50%,问第2小时直播带货额是( )万元。
A.1580 B.1600
C.1860 D.2000
【解析】该题若直接将所求第2小时直播带货额设为未知数,完全没办法建立等量关系。通过分析,A、B和C类产品的总销售额分别氛围第1小时、第2小时和第三小时,且第1小时中A、C产品的销售额都与B产品的销售额有关系,这时可将B产品第1小时的销售额设为x元。通过梳理关系可建立如下表格
通过最后1小时共带货3090万元,建立等量关系并化简得4(x-50)+2.7x+2.7x=3090,解出x=350,代入第2小时总销售额表达式2(x-50)+1.8x+1.8x=5.6x-100=350脳5.6-100=1860元,选择C选项。该题就是通过设中间桥梁量为未知数,然如找到等量关系进行快速求解,各相关量表示清晰,含义清楚,计算简便,能够有效的缩短解题时间。
第二,根据比例份数设未知数。当题目中出现了部分占总数的的情况,如果直接将总数设为未知数,部分就需要分数表示出来,加大了计算难度。通过数字特性法可知,总数是n的倍数,即可设总数为nx,每份为x。请看例2。
【例2】年终某大型企业的甲、乙、丙三个部门评选优秀员工,已知甲、乙部门优秀员工数分别占三个部门总优秀员工数的1/3和2/5,且甲部门优秀员工数比丙部门的多12人,问三个部门共评选出优秀员工多少人?
A.120 B.150
C.160 D.180
【解析】通过题干条件"甲、乙部门优秀员工数分别占三个部门总优秀员工数的1/3和2/5"可知,三个部门总优秀员工数既是3的倍数、又是5的倍数,因此可将总优秀员工数设为15x人。进一步可将甲乙各部门优秀员工数表示为5x人和6x人,那么丙部门优秀员工数为4x(15x-5x-6x)人。又根据"甲部门优秀员工数比丙部门的多12人"可列等量关系为5x-4x=12,解得x=12人。即每份为12人,总共15份,所以求得三个部门共评选出优秀员工180人。该题就是典型的通过比例设份数的思想,避免了其中的分数计算,从而使得计算更加简便。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 第1章 化工设计基本知识 在线思维导图免费制作,点击“编辑”按钮,可对 第1章 化工设计基本知识 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:70ec0519ed26419068a32a511862aadd






 上海工商
上海工商