排列组合之隔板法思维导图
自从2020年黑龙江省考开始,数量关系模块加大了对于排列组合与概率的考查力度,这对于精通这两个模块的同学也是个振奋人心的消息。
树图思维导图提供 排列组合之隔板法 在线思维导图免费制作,点击“编辑”按钮,可对 排列组合之隔板法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6a1a9784ec73eeb705024d059e9681cd
思维导图大纲
排列组合之隔板法思维导图模板大纲
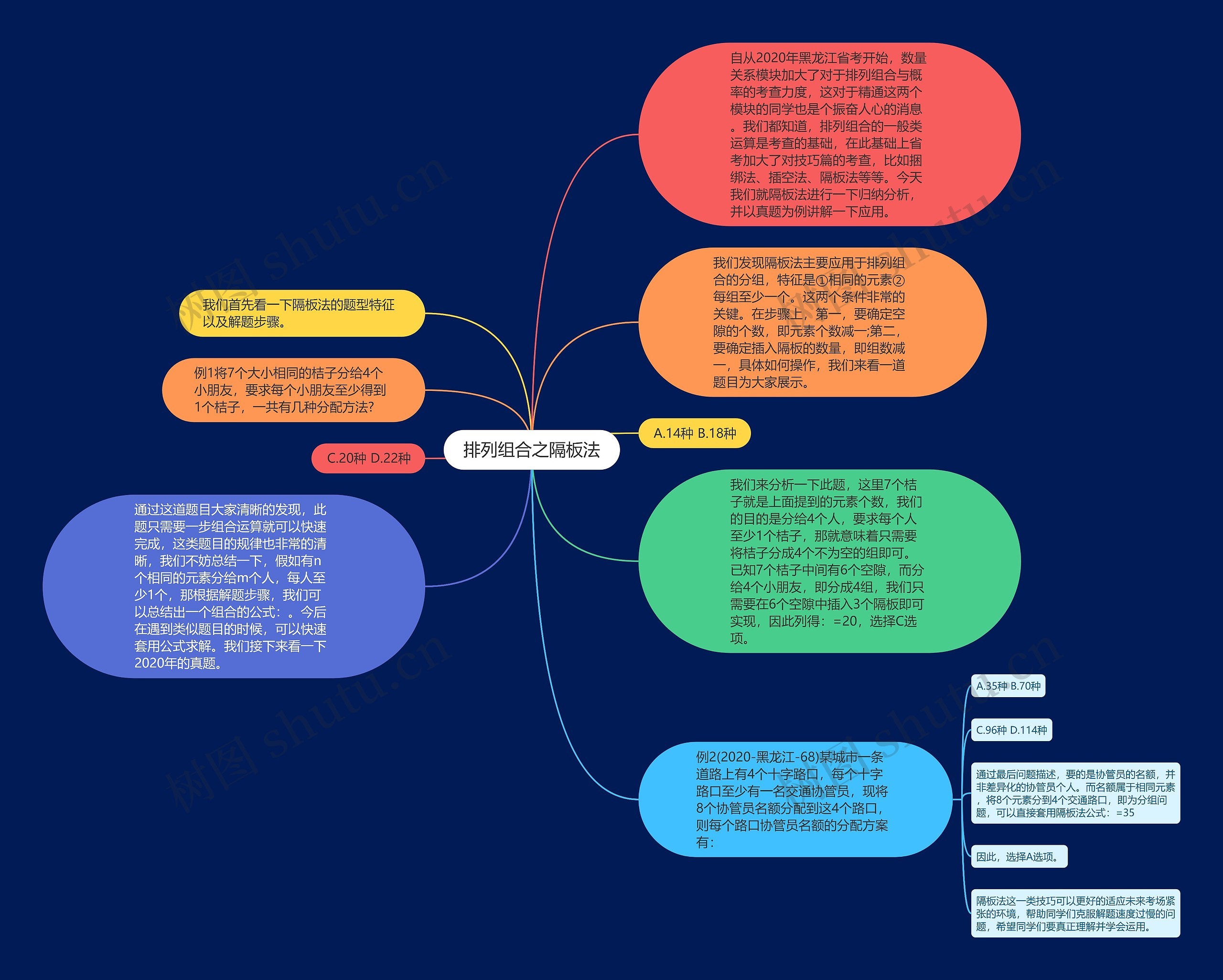
自从2020年黑龙江省考开始,数量关系模块加大了对于排列组合与概率的考查力度,这对于精通这两个模块的同学也是个振奋人心的消息。我们都知道,排列组合的一般类运算是考查的基础,在此基础上省考加大了对技巧篇的考查,比如捆绑法、插空法、隔板法等等。今天我们就隔板法进行一下归纳分析,并以真题为例讲解一下应用。
我们首先看一下隔板法的题型特征以及解题步骤。
我们发现隔板法主要应用于排列组合的分组,特征是①相同的元素②每组至少一个。这两个条件非常的关键。在步骤上,第一,要确定空隙的个数,即元素个数减一;第二,要确定插入隔板的数量,即组数减一,具体如何操作,我们来看一道题目为大家展示。
例1将7个大小相同的桔子分给4个小朋友,要求每个小朋友至少得到1个桔子,一共有几种分配方法?
A.14种 B.18种
C.20种 D.22种
我们来分析一下此题,这里7个桔子就是上面提到的元素个数,我们的目的是分给4个人,要求每个人至少1个桔子,那就意味着只需要将桔子分成4个不为空的组即可。已知7个桔子中间有6个空隙,而分给4个小朋友,即分成4组,我们只需要在6个空隙中插入3个隔板即可实现,因此列得:=20,选择C选项。
通过这道题目大家清晰的发现,此题只需要一步组合运算就可以快速完成,这类题目的规律也非常的清晰,我们不妨总结一下,假如有n个相同的元素分给m个人,每人至少1个,那根据解题步骤,我们可以总结出一个组合的公式:。今后在遇到类似题目的时候,可以快速套用公式求解。我们接下来看一下2020年的真题。
例2(2020-黑龙江-68)某城市一条道路上有4个十字路口,每个十字路口至少有一名交通协管员,现将8个协管员名额分配到这4个路口,则每个路口协管员名额的分配方案有:
A.35种 B.70种
C.96种 D.114种
通过最后问题描述,要的是协管员的名额,并非差异化的协管员个人。而名额属于相同元素,将8个元素分到4个交通路口,即为分组问题,可以直接套用隔板法公式:=35
因此,选择A选项。
隔板法这一类技巧可以更好的适应未来考场紧张的环境,帮助同学们克服解题速度过慢的问题,希望同学们要真正理解并学会运用。




















 上海工商
上海工商