高中数学《方程的根与函数的零点》说课稿思维导图
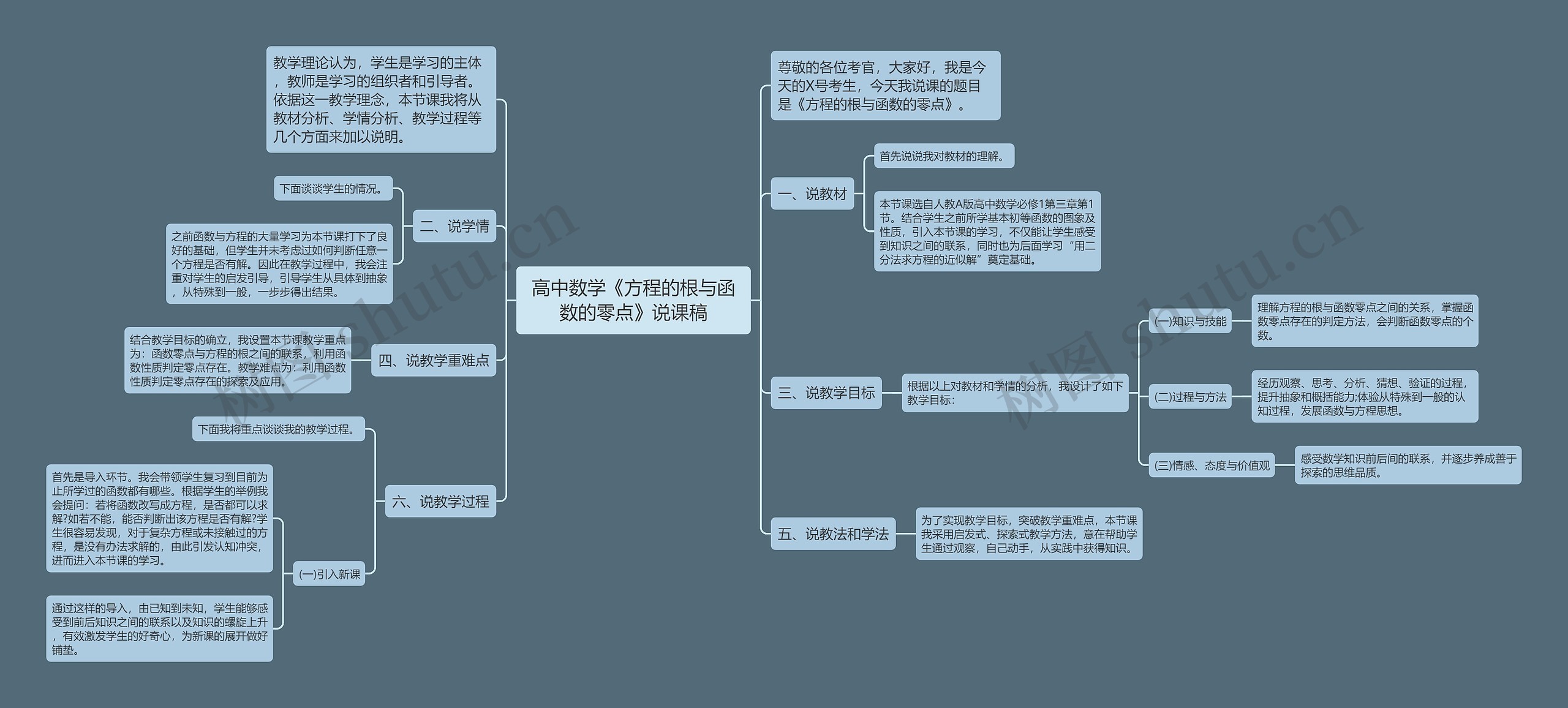
大家好,我是的X号考生,我将为大家介绍高中数学《方程的根与函数的零点》说课稿思维导图中的知识点,我们在教材分析中了解到,本次是取自人教A版高中数学必修1第三章第1节,目的是为了让学生了解知识之间的联系和为后续“用二分法求方程的近似解”提供基础,在学情分析中,注意到学生之前已经学习了许多函数与方程的知识,但他们缺乏如何判断方程是否有解的能力。在教学目标中,要让学生掌握函数零点存在的判定方法和从特殊到一般的认知过程。在教学重难点中,需要教授学生函数零点与方程的根之间的联系和利用函数性质判定零点的存在,在教学过程中,采用启发式、探索式教学方法让学生通过观察和实践获得知识,同时从已知到未知引导学生理解前后知识之间的联系,并激发学生的好奇心。
思维导图大纲
高中数学《方程的根与函数的零点》说课稿思维导图模板大纲
尊敬的各位考官,大家好,我是今天的X号考生,今天我说课的题目是《方程的根与函数的零点》。
教学理论认为,学生是学习的主体,教师是学习的组织者和引导者。依据这一教学理念,本节课我将从教材分析、学情分析、教学过程等几个方面来加以说明。
一、说教材
首先说说我对教材的理解。
本节课选自人教A版高中数学必修1第三章第1节。结合学生之前所学基本初等函数的图象及性质,引入本节课的学习,不仅能让学生感受到知识之间的联系,同时也为后面学习“用二分法求方程的近似解”奠定基础。
二、说学情
下面谈谈学生的情况。
之前函数与方程的大量学习为本节课打下了良好的基础,但学生并未考虑过如何判断任意一个方程是否有解。因此在教学过程中,我会注重对学生的启发引导,引导学生从具体到抽象,从特殊到一般,一步步得出结果。
三、说教学目标
根据以上对教材和学情的分析,我设计了如下教学目标:
(一)知识与技能
理解方程的根与函数零点之间的关系,掌握函数零点存在的判定方法,会判断函数零点的个数。
(二)过程与方法
经历观察、思考、分析、猜想、验证的过程,提升抽象和概括能力;体验从特殊到一般的认知过程,发展函数与方程思想。
(三)情感、态度与价值观
感受数学知识前后间的联系,并逐步养成善于探索的思维品质。
四、说教学重难点
结合教学目标的确立,我设置本节课教学重点为:函数零点与方程的根之间的联系,利用函数性质判定零点存在。教学难点为:利用函数性质判定零点存在的探索及应用。
五、说教法和学法
为了实现教学目标,突破教学重难点,本节课我采用启发式、探索式教学方法,意在帮助学生通过观察,自己动手,从实践中获得知识。
六、说教学过程
下面我将重点谈谈我的教学过程。
(一)引入新课
首先是导入环节。我会带领学生复习到目前为止所学过的函数都有哪些。根据学生的举例我会提问:若将函数改写成方程,是否都可以求解?如若不能,能否判断出该方程是否有解?学生很容易发现,对于复杂方程或未接触过的方程,是没有办法求解的,由此引发认知冲突,进而进入本节课的学习。
通过这样的导入,由已知到未知,学生能够感受到前后知识之间的联系以及知识的螺旋上升,有效激发学生的好奇心,为新课的展开做好铺垫。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a












 上海工商
上海工商