不定积分思维导图
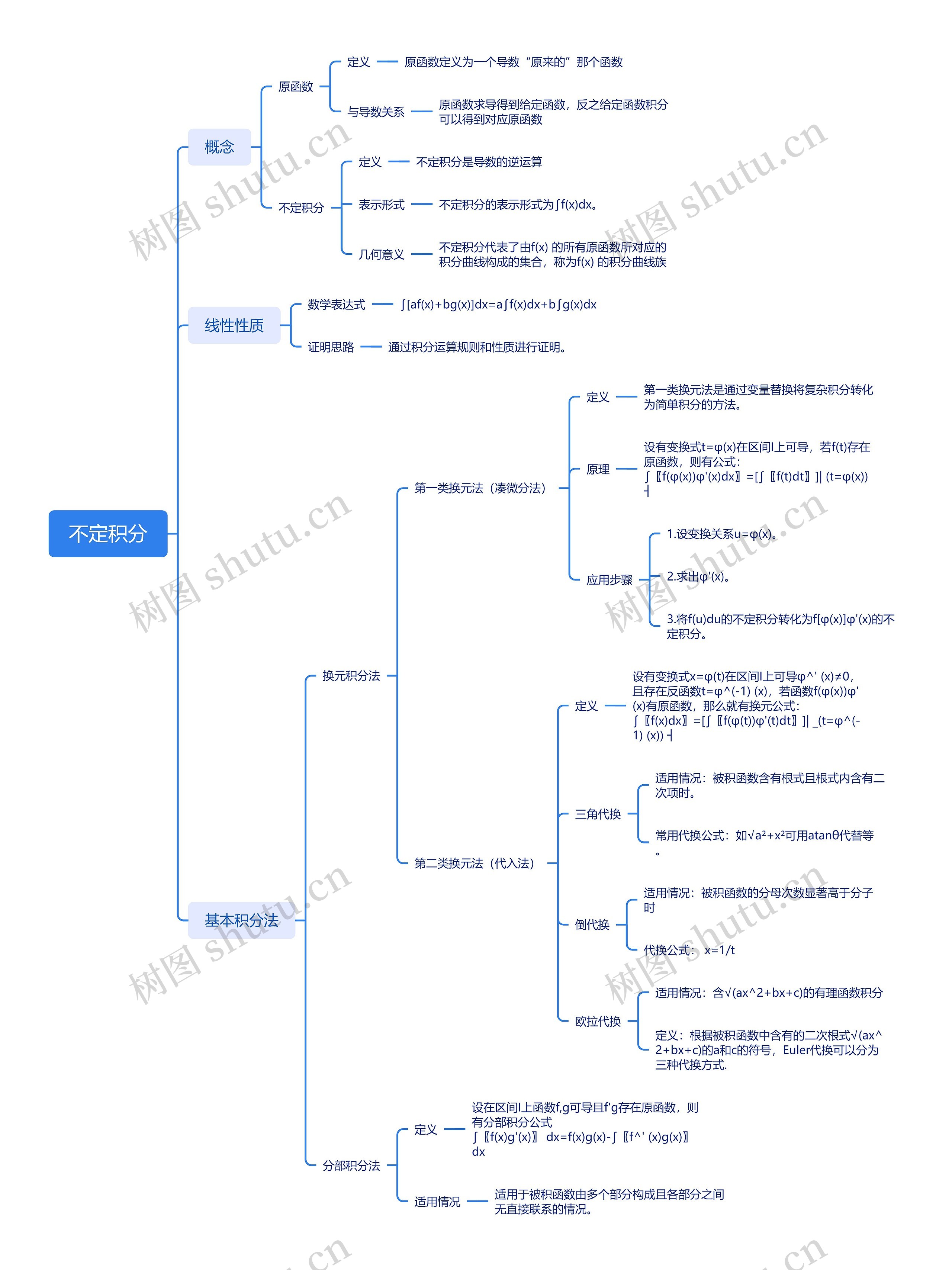
不定积分内容详述
树图思维导图提供 不定积分 在线思维导图免费制作,点击“编辑”按钮,可对 不定积分 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9a16f649c3f72de156804aebd54a9a9f
思维导图大纲
不定积分思维导图模板大纲
概念
原函数
定义
原函数定义为一个导数“原来的”那个函数
与导数关系
原函数求导得到给定函数,反之给定函数积分可以得到对应原函数
不定积分
定义
不定积分是导数的逆运算
表示形式
不定积分的表示形式为∫f(x)dx。
几何意义
不定积分代表了由f(x) 的所有原函数所对应的积分曲线构成的集合,称为f(x) 的积分曲线族
线性性质
数学表达式
∫[af(x)+bg(x)]dx=a∫f(x)dx+b∫g(x)dx
证明思路
通过积分运算规则和性质进行证明。
基本积分法
换元积分法
第一类换元法(凑微分法)
定义
第一类换元法是通过变量替换将复杂积分转化为简单积分的方法。
原理
设有变换式t=φ(x)在区间I上可导,若f(t)存在原函数,则有公式: ∫〖f(φ(x))φ'(x)dx〗=[∫〖f(t)dt〗]| (t=φ(x)) ┤
应用步骤
1.设变换关系u=φ(x)。
2.求出φ'(x)。
3.将f(u)du的不定积分转化为f[φ(x)]φ'(x)的不定积分。
第二类换元法(代入法)
定义
设有变换式x=φ(t)在区间I上可导φ^' (x)≠0,且存在反函数t=φ^(-1) (x),若函数f(φ(x))φ'(x)有原函数,那么就有换元公式: ∫〖f(x)dx〗=[∫〖f(φ(t))φ'(t)dt〗]| _(t=φ^(-1) (x)) ┤
三角代换
适用情况:被积函数含有根式且根式内含有二次项时。
常用代换公式:如√a²+x²可用atanθ代替等。
倒代换
适用情况:被积函数的分母次数显著高于分子时
代换公式: x=1/t
欧拉代换
适用情况:含√(ax^2+bx+c)的有理函数积分
定义:根据被积函数中含有的二次根式√(ax^2+bx+c)的a和c的符号,Euler代换可以分为三种代换方式.
分部积分法
定义
设在区间I上函数f,g可导且f'g存在原函数,则有分部积分公式 ∫〖f(x)g'(x)〗 dx=f(x)g(x)-∫〖f^' (x)g(x)〗 dx
适用情况
适用于被积函数由多个部分构成且各部分之间无直接联系的情况。
相关思维导图模板

树图思维导图提供 积分思维脑图 在线思维导图免费制作,点击“编辑”按钮,可对 积分思维脑图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c3c017382628acd9f38063ee08f8034f

树图思维导图提供 2023考研数学定积分与不定积分知识点整理 在线思维导图免费制作,点击“编辑”按钮,可对 2023考研数学定积分与不定积分知识点整理 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d0ff2eac8fc9b0392c2f5308f57f56f1
















 上海工商
上海工商