六年级上册数学思维导图，简单好看的模板分享

编辑by脆脆鲨

六年级上册数学思维导图怎么画？学生们在进入到六年级之后，发现数学的难度好像又变大了？逐步增加难度是很正常的现象。六年级过后即将升入初中，为了良好地与中学衔接，更加需要我们打好小学阶段的数学基础。为此，小编在【树图-帮助中心-校园教育】为大家整理了一份六年级上册数学思维导图，希望学生们能够借助这份导图，对知识点有一个整体上的把握。

一、为什么用思维导图梳理小学六年级上册数学的知识

在梳理六年级数学的相关内容时，一般会用摘录已经注释的方式从上往下依序说明相关知识内容。而利用思维导图工具梳理生物知识，则可以结合思维导图工具的特点在整体在基础上系统性地梳理英语的相关内容，以便逻辑有序地展开梳理，并呈现各知识点之间的逻辑关系。

  当然了，除了六年级数学知识点的思维导图外，思维导图还可用于其它诸多场景。如读书笔记、个人规划、工作总结、旅行清单等。

二、如何用思维导图整理六年级上册数学的知识

思维导图给我们提供了一种途径，这是总结归纳知识较为合适的工具，利用思维导图图文并用的特点，帮助学生建立整体思维方向，梳理数学科目中的方法、规律，能够更轻松地理解和记忆知识点。

思维导图作为一种以层级特点梳理发散性内容的工具，首先需要确定六上数学的相关知识点内容。在利用思维导图工具梳理六上数学时，注意各层级节点之间的的逻辑关系，有序地梳理各节点内容。

三、如何画六年级上册数学的思维导图

想要绘制六上数学的思维导图，通常可以使用树图思维导图进行，这是一款适用于电脑端绘图的工具，打开编辑器后将需要梳理的内容填充至节点即可简单制图，同时还带有诸多“节点样式”与“主题风格”功能辅助绘制精美好看的思维导图。是一款简单好用的思维导图绘制工具。下面给大家简单分享用树图思维导图绘制六上数学思维导图的方法。

（1）首先通过树图思维导图工具【新建文件-选择合适的结构】并进入到对应的编辑页面；

（2）接下来以层层递进的方式将需要梳理的物理知识相关内容呈现至节点。梳理基本内容；

（3）随后还可以利用插入图标、备注、链接、关系线、概要等功能进一步思维导图的内容；

（4）而后还可以试着借助主题、样式、一键美化等相关功能对思维导图进行适当的优化处理；

（5）当物理知识的思维导图绘制完毕后，直接将图示“保存”至账号云端，或“导出”为png、pdf、jpg等格式即可。

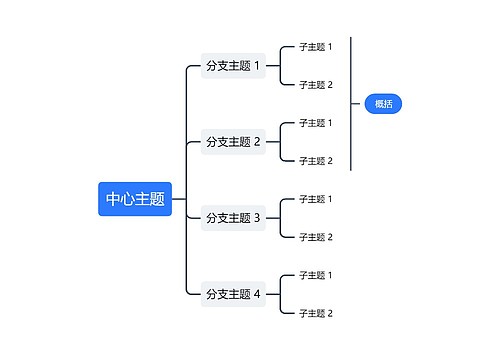
四、大纲

人教版数学六年级上册知识点汇总

第五单元 圆

圆的特征

圆是平面内封闭曲线围成的平面图形。

圆的特征：外形美观，易滚动。

圆心O

圆中心的点叫做圆心．圆心一般用字母O表示。

半径r

连接圆心到圆上任意一点的线段叫做半径。在同一个圆里，有无数条半径，且所有的半径都相等。半径确定圆的大小。

直径d

通过圆心且两端都在圆上的线段叫做直径。在同一个圆里，有无数条直径，且所有的直径都相等。直径是圆内最长的线段。

等圆

半径相等的圆叫做等圆，等圆通过平移可以完全重合。

同心圆

圆心重合、半径不等的两个圆叫做同心圆。

圆的周长C

圆的周长(c)=直径(d)×圆周率(π)周长公式

C=πd,

C=2πr

圆的面积S

圆的面积=圆的周长的一半（πr）×圆的半径（r）

S圆=πr×r=πr2

第二单元 位置与方向（二）

什么是数对？

数对：由两个数组成，中间用逗号隔开，用括号括起来。括号里面的数由左至右为列数和行数，即“先列后行”。

确定一个点的位置。经度和纬度就是这个原理。

确定一个点的位置。经度和纬度就是这个原理。

确定物体位置的方法

（1）、先找观测点；

（2）、再定方向（看方向夹角的度数）；

（3）、最后确定距离（看比例尺）。

第六单元 百分数（一）

百分数的意义

表示一个数是另一个数的百分之几的数叫做百分数。百分数又叫百分比或百分率，百分数不能带单位。

百分数和分数的区别和联系

联系：都可以用来表示两个量的倍比关系。

区别：意义不同：百分数只表示倍比关系，不表示具体数量，所以不能带单位。分数不仅表示倍比关系，还能带单位表示具体数量。百分数的分子可以是小数，分数的分子只可以是整数。

小数、分数、百分数之间的互化

百分数化小数：小数点向左移动两位，去掉“%”。

小数化百分数：小数点向右移动两位，添上“%”。\n

百分数化分数：先把百分数写成分母是100的分数，然后再化简成最简分数。

分数化百分数：分子除以分母得到小数，（除不尽的保留三位小数）然后化成百分数。

小数化分数：把小数成分母是10、100、1000等的分数再化简。

分数化小数：分子除以分母。

百分数应用题

百分数

求常见的百分率,如：达标率、及格率、成活率、发芽率、出勤率等

求百分率就是求一个数是另一个数的百分之几。

求一个数比另一个数多（或少）百分之几，实际生活中，人们常用增加了百分之几、减少了百分之几、节约了百分之几等来表示增加、或减少的幅度。

求甲比乙多百分之几：（甲-乙）÷乙

求乙比甲少百分之几：（甲-乙）÷甲

求一个数的百分之几是多少。

一个数（单位“1”）×百分率

已知一个数的百分之几是多少，求这个数。

部分量÷百分率=一个数（单位“1”）

折扣、打折的意义

几折就是十分之几也就是百分之几十

八折=八成=十分之八=百分之八十=0.8

八五折=八成五=十分之八点五=百分之八十五=0.85

五折=五成=十分之五=百分之五十=0.5=半价

利率

存入银行的钱叫做本金。

取款时银行多支付的钱叫做利息。

利息与本金的比值叫做利率。

利息=本金×利率×时间

税后利息=利息-利息的应纳税额=利息-利息×5%

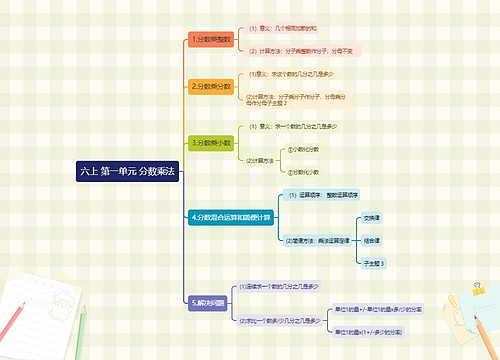
第三单元 分数的除法

分数除法的意义

分数除法是分数乘法的逆运算，已知两个数的积与其中一个因数，求另一个因数的运算。

分数除法计算法则：除以一个数（0除外），等于乘上这个数的倒数。

被除数÷除数=被除数×除数的倒数。

除法转化成乘法时，被除数一定不能变，“÷”变成“×”，除数变成它的倒数。

分数除法算式中出现小数、带分数时要先化成分数、假分数再计算。

被除数与商的变化规律：

①除以大于1的数，商小于被除数：a÷b=c 当b>1时，c

②除以小于1的数，商大于被除数：a÷b=c 当b

③除以等于1的数，商等于被除数：a÷b=c 当b=1时，c=a

分数除法混合运算

混合运算用梯等式计算，等号写在第一个数字的左下角。

运算顺序：

①连除：同级运算，按照从左往右的顺序进行计算；或者先把所有除法转化成乘法再计算；或者依据“除以几个数，等于乘上这几个数的积”的简便方法计算。加、减法为一级运算，乘、除法为二级运算。

②混合运算：没有括号的先乘、除后加、减，有括号的先算括号里面，再算括号外面。

（a±b）÷c=a÷c±b÷c

第八单元 数学广角--数与形

2＋4＋6＋8＋10＋12＋14＋16＋18＋20＝（110）

规律：从2开始的n个连续偶数的和等于n×(n＋1)。

10×(10＋1)＝10×11＝110

第七单元 扇形统计图的意义

扇形统计图的意义

用整个圆的面积表示总数，用圆内各个扇形面积表示各部分数量同总数之间关系，也就是各部分数量占总数的百分比，因此也叫百分比图。

常用统计图的优点

条形统计图直观显示每个数量的多少。

折线统计图不仅直观显示数量的增减变化，还可清晰看出各个数量的多少。

扇形统计图直观显示部分和总量的关系。

第一单元 分数乘法

分数乘法意义

分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

“分数乘整数”指的是第二个因数必须是整数，不能是分数。

一个数乘分数的意义就是求一个数的几分之几是多少。

“一个数乘分数”指的是第二个因数必须是分数，不能是整数。（第一个因数是什么都可以）

分数乘法计算法则

分数乘整数的运算法则是：

分子与整数相乘，分母不变。

分数乘分数的运算法则是

用分子相乘的积做分子，分母相乘的积做分母。（分子乘分子，分母乘分母）

分数乘法混合运算

分数乘法混合运算顺序与整数相同，先乘、除后加、减，有括号的先算括号里面的，再算括号外面的。

整数乘法运算定律对分数乘法同样适用；运算定律可以使一些计算简便。

乘法交换律：a×b=b×a

乘法结合律：(a×b)×c=a×(b×c)\n

乘法分配律：a×(b±c)=a×b±a×c

倒数的意义：乘积为1的两个数互为倒数。

判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为“1”。例如：a×b=1则a、b互为倒数。

分数乘法应用题——用分数乘法解决问题

求一个数的几分之几是多少？（用乘法）

已知单位“1”的量，求单位“1”的量的几分之几是多少，用单位“1”的量与分数相乘。

巧找单位“1”的量：在含有分数（分率）的语句中，分率前面的量就是单位“1”对应的量，或者“占”“是”“比”字后面的量是单位“1”。

什么是速度？

速度=路程÷时间

单位时间指的是1小时1分钟1秒等这样的大小为1的时间单位，每分钟、每小时、每秒钟等。

求甲比乙多（少）几分之几？

多：（甲-乙）÷乙

少：（乙-甲）÷乙

第四单元 比

比

两个数相除也叫两个数的比

比式中，比号（∶）前面的数叫前项，比号后面的项叫做后项，比号相当于除号，比的前项除以后项的商叫做比值。

比如：3：4：5读作：3比4比5\n

比的基本性质

比的前项和后项同时乘以或除以相同的数（0除外），比值不变。

求比值

把比号写成除号再计算，结果是一个数（或分数），相当于商，不是比。

比和除法、分数的区别

除法：被除数除号（÷） 除数（不能为0） 商不变性质 除法是一种运算

商不变性质：被除数和除数同时乘或除以相同的数（0除外），商不变。

分数：分子分数线（—）分母（不能为0） 分数的基本性质 分数是一个数

分数的基本性质：分子和分母同时乘或除以相同的数（0除外），分数的大小不变。

比：前项比号（∶） 后项（不能为0） 比的基本性质 比表示两个数的关系