2024考研数学重难点有哪些?含常考题型思维导图
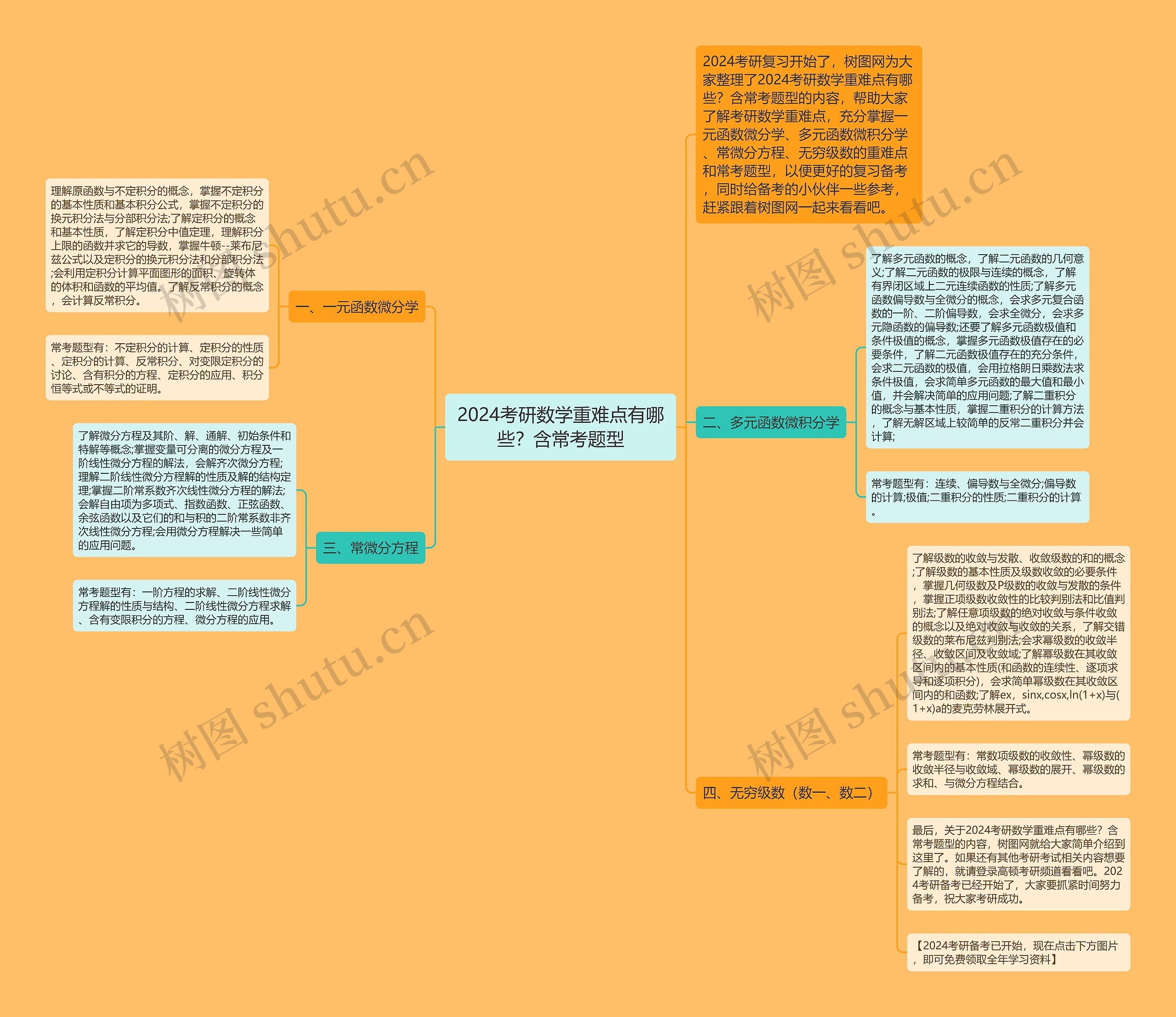
2024考研数学复习已经开始了,对于备考的来说,了解数学重难点和常考题型是非常关键的,因此树图网为大家整理了一份思维导图,涵盖了一元函数微分学、多元函数微积分学、常微分方程、无穷级数。并详细介绍了常考题型的解法和应用。在一元函数微分学中,需要了解不定积分、定积分、反常积分等内容,掌握积分的计算方法和应用,在多元函数微积分学中,需要掌握偏导数、全微分、极值、二重积分等内容,并能够解决简单的应用问题,在常微分方程中,需要了解微分方程的阶、解、通解、特解。并掌握一阶和二阶微分方程的解法,最后在无穷级数中,需要了解级数收敛与发散、幂级数、麦克劳林展开等内容,和他们的应用。
思维导图大纲
2024考研数学重难点有哪些?含常考题型思维导图模板大纲
2024考研复习开始了,树图网为大家整理了2024考研数学重难点有哪些?含常考题型的内容,帮助大家了解考研数学重难点,充分掌握一元函数微分学、多元函数微积分学、常微分方程、无穷级数的重难点和常考题型,以便更好的复习备考,同时给备考的小伙伴一些参考,赶紧跟着树图网一起来看看吧。
一、一元函数微分学
理解原函数与不定积分的概念,掌握不定积分的基本性质和基本积分公式,掌握不定积分的换元积分法与分部积分法;了解定积分的概念和基本性质,了解定积分中值定理,理解积分上限的函数并求它的导数,掌握牛顿--莱布尼兹公式以及定积分的换元积分法和分部积分法;会利用定积分计算平面图形的面积、旋转体的体积和函数的平均值。了解反常积分的概念,会计算反常积分。
常考题型有:不定积分的计算、定积分的性质、定积分的计算、反常积分、对变限定积分的讨论、含有积分的方程、定积分的应用、积分恒等式或不等式的证明。
二、多元函数微积分学
了解多元函数的概念,了解二元函数的几何意义;了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质;了解多元函数偏导数与全微分的概念,会求多元复合函数的一阶、二阶偏导数,会求全微分,会求多元隐函数的偏导数;还要了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决简单的应用问题;了解二重积分的概念与基本性质,掌握二重积分的计算方法,了解无解区域上较简单的反常二重积分并会计算;
常考题型有:连续、偏导数与全微分;偏导数的计算;极值;二重积分的性质;二重积分的计算。
三、常微分方程
了解微分方程及其阶、解、通解、初始条件和特解等概念;掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程;理解二阶线性微分方程解的性质及解的结构定理;掌握二阶常系数齐次线性微分方程的解法;会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程;会用微分方程解决一些简单的应用问题。
常考题型有:一阶方程的求解、二阶线性微分方程解的性质与结构、二阶线性微分方程求解、含有变限积分的方程、微分方程的应用。
四、无穷级数(数一、数二)
了解级数的收敛与发散、收敛级数的和的概念;了解级数的基本性质及级数收敛的必要条件,掌握几何级数及P级数的收敛与发散的条件,掌握正项级数收敛性的比较判别法和比值判别法;了解任意项级数的绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系,了解交错级数的莱布尼兹判别法;会求幂级数的收敛半径、收敛区间及收敛域;了解幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分),会求简单幂级数在其收敛区间内的和函数;了解ex,sinx,cosx,ln(1+x)与(1+x)a的麦克劳林展开式。
常考题型有:常数项级数的收敛性、幂级数的收敛半径与收敛域、幂级数的展开、幂级数的求和、与微分方程结合。
最后,关于2024考研数学重难点有哪些?含常考题型的内容,树图网就给大家简单介绍到这里了。如果还有其他考研考试相关内容想要了解的,就请登录高顿考研频道看看吧。2024考研备考已经开始了,大家要抓紧时间努力备考,祝大家考研成功。
【2024考研备考已开始,现在点击下方图片,即可免费领取全年学习资料】
相关思维导图模板

树图思维导图提供 第1章 化工设计基本知识 在线思维导图免费制作,点击“编辑”按钮,可对 第1章 化工设计基本知识 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:70ec0519ed26419068a32a511862aadd


树图思维导图提供 抓住重点 在线思维导图免费制作,点击“编辑”按钮,可对 抓住重点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826


















 上海工商
上海工商