初一浙教版数学上册复习提纲2023春思维导图
初一浙教版数学上册复习提纲2023春。以下是初一浙教版数学上册复习提纲2023春,供大家参考。
树图思维导图提供 初一浙教版数学上册复习提纲2023春 在线思维导图免费制作,点击“编辑”按钮,可对 初一浙教版数学上册复习提纲2023春 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b04569818bc0358d0c99b0c3da4a02c4
思维导图大纲
初一浙教版数学上册复习提纲2023春思维导图模板大纲
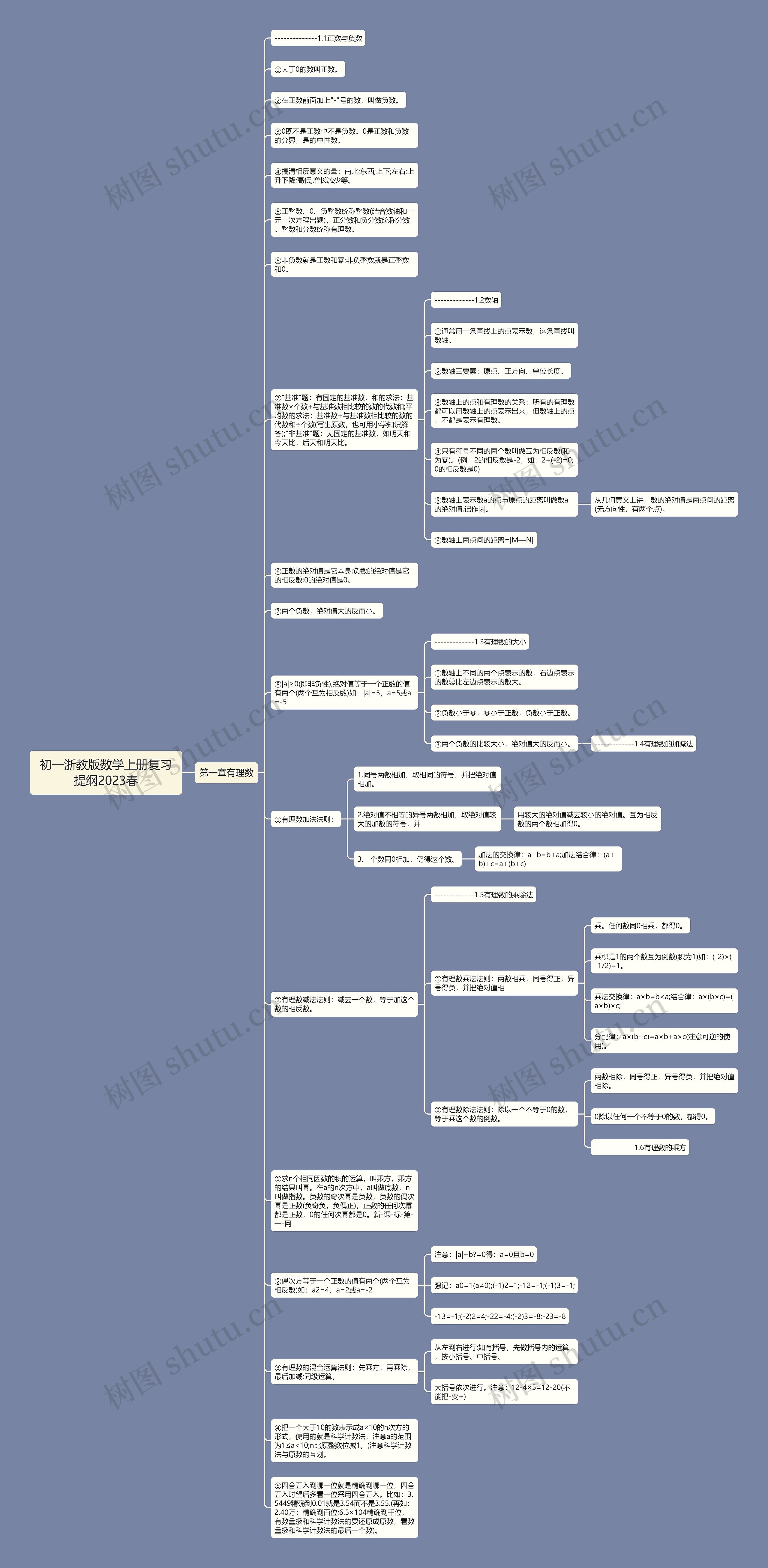
第一章有理数
--------------1.1正数与负数
①大于0的数叫正数。
②在正数前面加上"-"号的数,叫做负数。
③0既不是正数也不是负数。0是正数和负数的分界,是的中性数。
④搞清相反意义的量:南北;东西;上下;左右;上升下降;高低;增长减少等。
⑤正整数、0、负整数统称整数(结合数轴和一元一次方程出题),正分数和负分数统称分数。整数和分数统称有理数。
⑥非负数就是正数和零;非负整数就是正整数和0。
⑦"基准"题:有固定的基准数,和的求法:基准数×个数+与基准数相比较的数的代数和;平均数的求法:基准数+与基准数相比较的数的代数和÷个数(写出原数,也可用小学知识解答);"非基准"题:无固定的基准数,如明天和今天比,后天和明天比。
-------------1.2数轴
①通常用一条直线上的点表示数,这条直线叫数轴。
②数轴三要素:原点、正方向、单位长度。
③数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴上的点,不都是表示有理数。
④只有符号不同的两个数叫做互为相反数(和为零)。(例:2的相反数是-2,如:2+(-2)=0;0的相反数是0)
⑤数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
从几何意义上讲,数的绝对值是两点间的距离(无方向性,有两个点)。
⑥数轴上两点间的距离=|M—N|
⑥正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。
⑦两个负数,绝对值大的反而小。
⑧|a|≥0(即非负性);绝对值等于一个正数的值有两个(两个互为相反数)如:|a|=5,a=5或a=-5
-------------1.3有理数的大小
①数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大。
②负数小于零,零小于正数,负数小于正数。
③两个负数的比较大小,绝对值大的反而小。
-------------1.4有理数的加减法
①有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并
用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。
加法的交换律:a+b=b+a;加法结合律:(a+b)+c=a+(b+c)
②有理数减法法则:减去一个数,等于加这个数的相反数。
-------------1.5有理数的乘除法
①有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相
乘。任何数同0相乘,都得0。
乘积是1的两个数互为倒数(积为1)如:(-2)×(-1/2)=1。
乘法交换律:a×b=b×a;结合律:a×(b×c)=(a×b)×c;
分配律:a×(b+c)=a×b+a×c(注意可逆的使用)。
②有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数。
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0的数,都得0。
-------------1.6有理数的乘方
①求n个相同因数的积的运算,叫乘方,乘方的结果叫幂。在a的n次方中,a叫做底数,n叫做指数。负数的奇次幂是负数,负数的偶次幂是正数(负奇负,负偶正)。正数的任何次幂都是正数,0的任何次幂都是0。新-课-标-第-一-网
②偶次方等于一个正数的值有两个(两个互为相反数)如:a2=4,a=2或a=-2
注意:|a|+b?=0得:a=0且b=0
强记:a0=1(a≠0);(-1)2=1;-12=-1;(-1)3=-1;
-13=-1;(-2)2=4;-22=-4;(-2)3=-8;-23=-8
③有理数的混合运算法则:先乘方,再乘除,最后加减;同级运算,
从左到右进行;如有括号,先做括号内的运算,按小括号、中括号、
大括号依次进行。注意:12-4×5=12-20(不能把-变+)
④把一个大于10的数表示成a×10的n次方的形式,使用的就是科学计数法,注意a的范围为1≤a<10;n比原整数位减1。(注意科学计数法与原数的互划。
⑤四舍五入到哪一位就是精确到哪一位,四舍五入时望后多看一位采用四舍五入。比如:3.5449精确到0.01就是3.54而不是3.55.(再如:2.40万:精确到百位;6.5×104精确到千位,有数量级和科学计数法的要还原成原数,看数量级和科学计数法的最后一个数)。

















 上海工商
上海工商