数学复习指导:解析几何专题热点思维导图
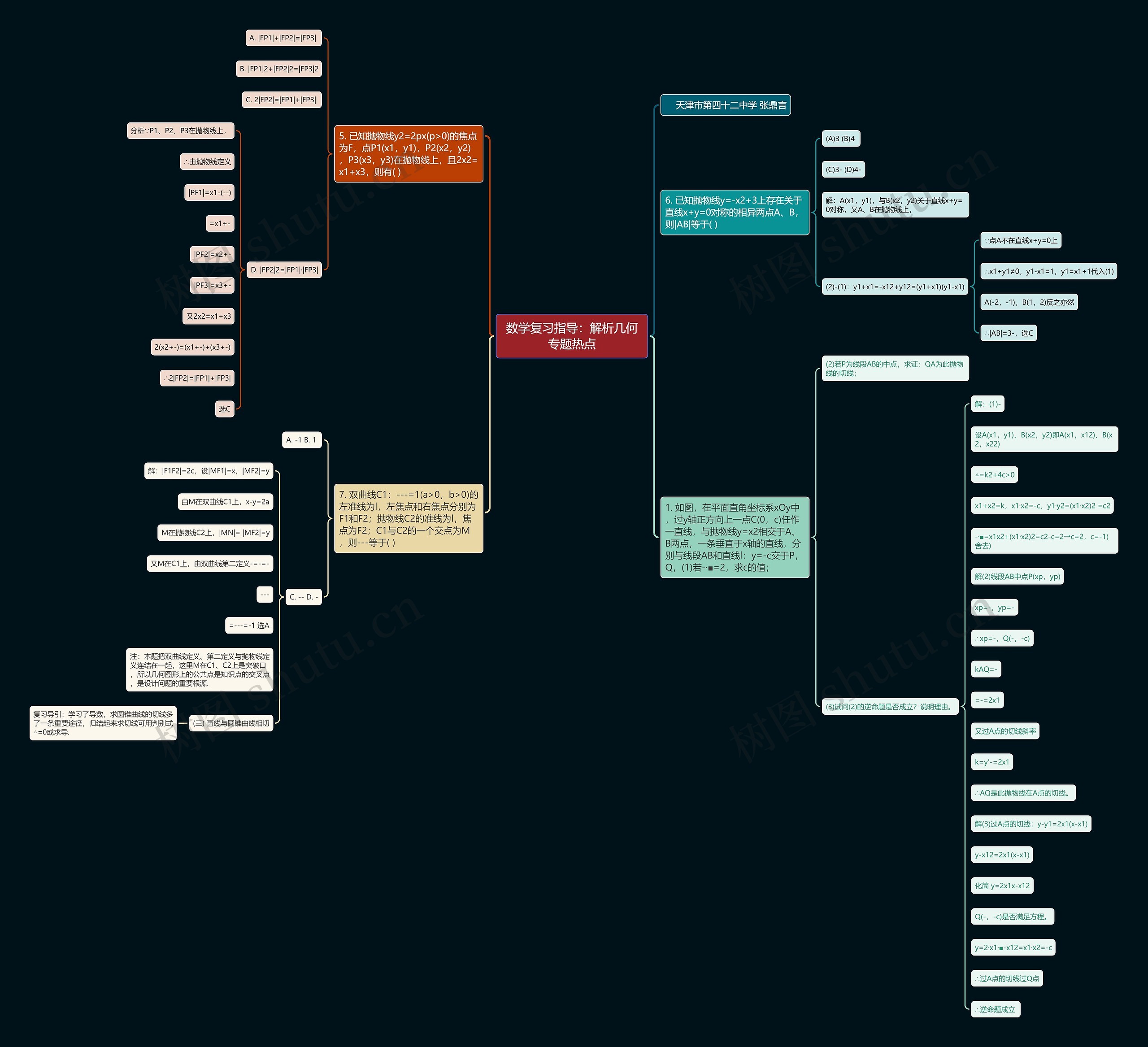
数学复习指导:解析几何专题热点思维导图,知识点如下:1.已知抛物线求焦点和点的坐标关系:使用抛物线的定义,可以求出抛物线上任意点与焦点的距离公式。根据已知条件,可以得出关于点P1、P2、P3和焦点F的等式,求解出等式的关系。
2.找寻对称点:可以通过求直线的对称点来确定抛物线上的两个相异点A、B。利用关于直线的对称性质,可以得到点A和点B的坐标。
3.双曲线/与抛物线的交点问题:通过双曲线和抛物线的定义和性质,可以求解特定条件下两个曲线的交点。具体分析给定条件,将点M在双曲线和抛物线上的关系结合起来,可以求解出等式的值。
还介绍了直线与圆锥曲线相切问题,包含通过求导和判别式来求解切线的问题。和通过给定条件,求出垂直于x轴的直线与线段和直线的交点的坐标。
对于给定直线与抛物线的交点,通过求证题目中的关系式,可以得出该直线是抛物线的切线的结论。但是对于逆命题是否成立,需要进一步分析和证明。
以上是“数学复习指导:解析几何专题热点思维导图”的知识点和相关问题的简述。希望对你的复习有所帮助!
思维导图大纲
数学复习指导:解析几何专题热点思维导图模板大纲
天津市第四十二中学 张鼎言
5. 已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1),P2(x2,y2),P3(x3,y3)在抛物线上,且2x2=x1+x3,则有( )
A. |FP1|+|FP2|=|FP3|
B. |FP1|2+|FP2|2=|FP3|2
C. 2|FP2|=|FP1|+|FP3|
D. |FP2|2=|FP1|·|FP3|
分析∵P1、P2、P3在抛物线上,
∴由抛物线定义
|PF1|=x1-(--)
=x1+-
|PF2|=x2+-
|PF3|=x3+-
又2x2=x1+x3
2(x2+-)=(x1+-)+(x3+-)
∴2|FP2|=|FP1|+|FP3|
选C
6. 已知抛物线y=-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于( )
(A)3 (B)4
(C)3- (D)4-
解:A(x1,y1),与B(x2,y2)关于直线x+y=0对称,又A、B在抛物线上,
(2)-(1):y1+x1=-x12+y12=(y1+x1)(y1-x1)
∵点A不在直线x+y=0上
∴x1+y1≠0,y1-x1=1,y1=x1+1代入(1)
A(-2,-1),B(1,2)反之亦然
∴|AB|=3-,选C
7. 双曲线C1:---=1(a>0,b>0)的左准线为l,左焦点和右焦点分别为F1和F2;抛物线C2的准线为l,焦点为F2;C1与C2的一个交点为M,则---等于( )
A. -1 B. 1
C. -- D. -
解:|F1F2|=2c,设|MF1|=x,|MF2|=y
由M在双曲线C1上,x-y=2a
M在抛物线C2上,|MN|= |MF2|=y
又M在C1上,由双曲线第二定义-=-=-
---
=---=-1 选A
注:本题把双曲线定义、第二定义与抛物线定义连结在一起,这里M在C1、C2上是突破口,所以几何图形上的公共点是知识点的交叉点,是设计问题的重要根源.
(三) 直线与圆锥曲线相切
复习导引:学习了导数,求圆锥曲线的切线多了一条重要途径,归结起来求切线可用判别式△=0或求导.
1. 如图,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A、B两点,一条垂直于x轴的直线,分别与线段AB和直线l:y=-c交于P,Q,(1)若-·■=2,求c的值;
(2)若P为线段AB的中点,求证:QA为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由。
解:(1)-
设A(x1,y1)、B(x2,y2)即A(x1,x12)、B(x2,x22)
△=k2+4c>0
x1+x2=k,x1·x2=-c,y1·y2=(x1·x2)2 =c2
-·■=x1x2+(x1·x2)2=c2-c=2→c=2,c=-1(舍去)
解(2)线段AB中点P(xp,yp)
xp=-,yp=-
∴xp=-,Q(-,-c)
kAQ=-
=-=2x1
又过A点的切线斜率
k=y'-=2x1
∴AQ是此抛物线在A点的切线。
解(3)过A点的切线:y-y1=2x1(x-x1)
y-x12=2x1(x-x1)
化简 y=2x1x-x12
Q(-,-c)是否满足方程。
y=2·x1·■-x12=x1·x2=-c
∴过A点的切线过Q点
∴逆命题成立
相关思维导图模板

树图思维导图提供 高考数学指导:解析几何专题热点复习 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学指导:解析几何专题热点复习 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:cf1d2879d34306fa76f1688303867611














 上海工商
上海工商