六年级数学思维导图 人教版
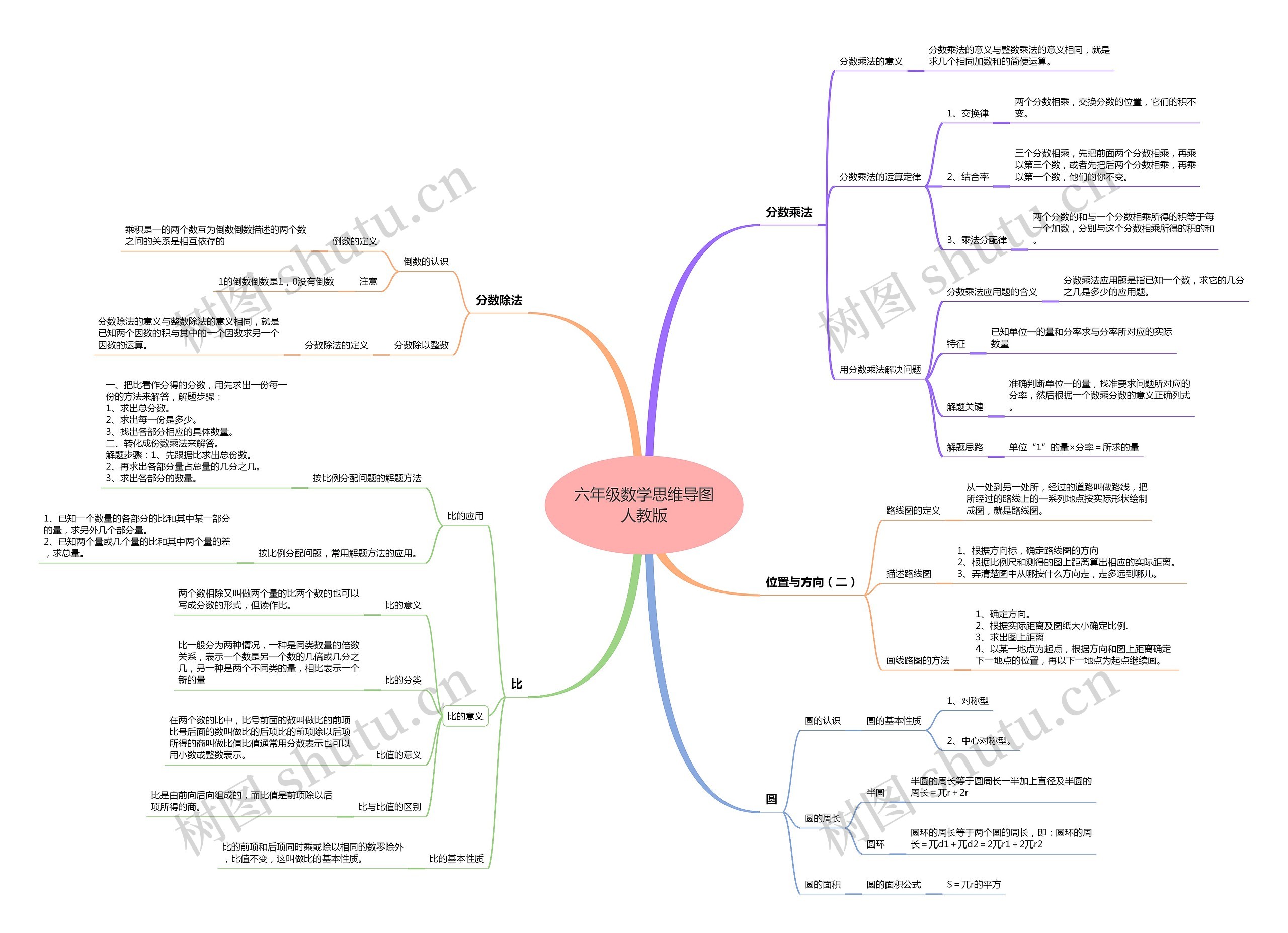
六年级数学人教版思维导图中的知识点包含分数乘法、分数乘法的意义和运算定律、用分数乘法解决问题、分数除法、倒数的认识、比的应用和意义、比值的计算方法和比的基本性质。分数乘法的意义与整数乘法相同,用于简单求几个相同加数和的运算,分数乘法的运算定律分别为交换律、结合率和乘法分配律,在用分数乘法解决问题时,需要准确判断单位一的量,找到对应的分率并正确列式。分数除法的意义也与整数除法相同,用于已知两个因数的积与其中一个因数求另一个因数的运算,比的使用常见于按比例分配问题,可通过转化成份数乘法的方式或先求出一份每份的方法来解答,比的基本性质包含前后项同时乘或除以相同的数比值不变,路线图则是由一系列道路上的地点绘制而成的图。
思维导图大纲
六年级数学思维导图 人教版思维导图模板大纲
分数乘法
分数乘法的意义
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
分数乘法的运算定律
1、交换律
两个分数相乘,交换分数的位置,它们的积不变。
2、结合率
三个分数相乘,先把前面两个分数相乘,再乘以第三个数,或者先把后两个分数相乘,再乘以第一个数,他们的你不变。
3、乘法分配律
两个分数的和与一个分数相乘所得的积等于每一个加数,分别与这个分数相乘所得的积的和。
用分数乘法解决问题
分数乘法应用题的含义
分数乘法应用题是指已知一个数,求它的几分之几是多少的应用题。
特征
已知单位一的量和分率求与分率所对应的实际数量
解题关键
准确判断单位一的量,找准要求问题所对应的分率,然后根据一个数乘分数的意义正确列式。
解题思路
单位“1”的量×分率=所求的量
分数除法
倒数的认识
倒数的定义
乘积是一的两个数互为倒数倒数描述的两个数之间的关系是相互依存的
注意
1的倒数倒数是1,0没有倒数
分数除以整数
分数除法的定义
分数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中的一个因数求另一个因数的运算。
比
比的应用
按比例分配问题的解题方法
一、把比看作分得的分数,用先求出一份每一 份的方法来解答,解题步骤: 1、求出总分数。 2、求出每一份是多少。 3、找出各部分相应的具体数量。 二、转化成份数乘法来解答。 解题步骤:1、先跟据比求出总份数。 2、再求出各部分量占总量的几分之几。 3、求出各部分的数量。
按比例分配问题,常用解题方法的应用。
1、已知一个数量的各部分的比和其中某一部分的量,求另外几个部分量。 2、已知两个量或几个量的比和其中两个量的差 ,求总量。
比的意义
比的意义
两个数相除又叫做两个量的比两个数的也可以写成分数的形式,但读作比。
比的分类
比一般分为两种情况,一种是同类数量的倍数关系,表示一个数是另一个数的几倍或几分之几,另一种是两个不同类的量,相比表示一个新的量
比值的意义
在两个数的比中,比号前面的数叫做比的前项比号后面的数叫做比的后项比的前项除以后项所得的商叫做比值比值通常用分数表示也可以用小数或整数表示。
比与比值的区别
比是由前向后向组成的,而比值是前项除以后项所得的商。
比的基本性质
比的前项和后项同时乘或除以相同的数零除外,比值不变,这叫做比的基本性质。
位置与方向(二)
路线图的定义
从一处到另一处所,经过的道路叫做路线,把所经过的路线上的一系列地点按实际形状绘制成图,就是路线图。
描述路线图
1、根据方向标,确定路线图的方向 2、根据比例尺和测得的图上距离算出相应的实际距离。 3、弄清楚图中从哪按什么方向走,走多远到哪儿。
画线路图的方法
1、确定方向。 2、根据实际距离及图纸大小确定比例. 3、求出图上距离 4、以某一地点为起点,根据方向和图上距离确定下一地点的位置,再以下一地点为起点继续画。
圆
圆的认识
圆的基本性质
1、对称型
2、中心对称型。
圆的周长
半圆
半圆的周长等于圆周长一半加上直径及半圆的周长=兀r+2r
圆环
圆环的周长等于两个圆的周长,即:圆环的周长=兀d1+兀d2=2兀r1+2兀r2
圆的面积
圆的面积公式
S=兀r的平方
相关思维导图模板


树图思维导图提供 小学三年级下册数学第一单元知识点归纳(人教版、苏教版) 在线思维导图免费制作,点击“编辑”按钮,可对 小学三年级下册数学第一单元知识点归纳(人教版、苏教版) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:afcb52693fe1ba7a7248f3dcf950abb1

树图思维导图提供 立方根人教版数学七年级上册教案 在线思维导图免费制作,点击“编辑”按钮,可对 立方根人教版数学七年级上册教案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d05b9775bee4307ea0ea29a9738aa9e0


















 上海工商
上海工商