高等数学函数知识点思维导图
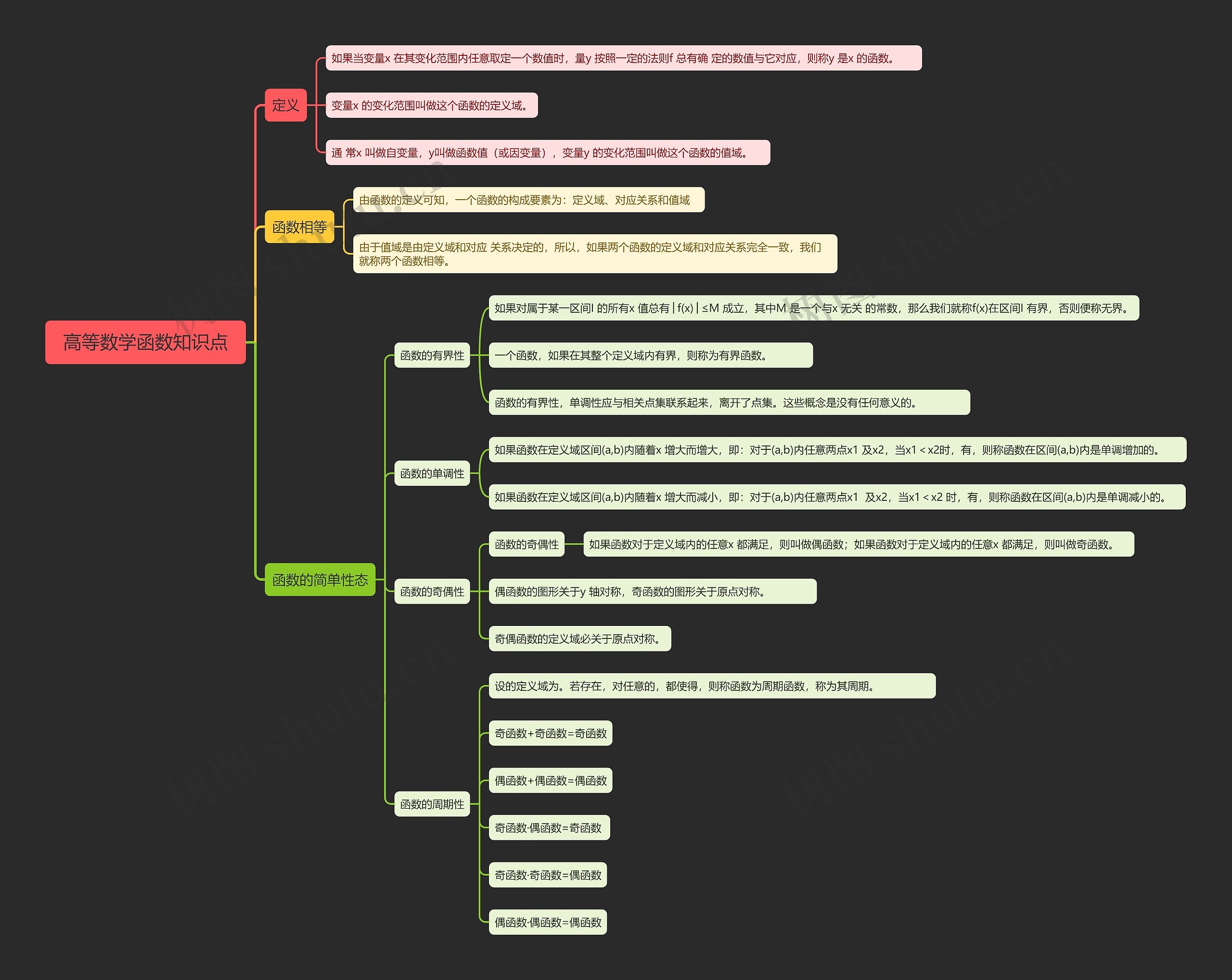
高等数学函数知识点思维导图涵盖函数的定义、函数相等、函数的简单性态、函数的有界性、函数的单调性、函数的奇偶性和函数的周期性几个知识点。函数的定义包含自变量与函数值之间的对应关系、定义域和值域,当两个函数的定义域和对应关系完全一致时,他相等,函数的简单性态包含有界性与无界性,函数的有界性需要与点集联系才有意义,有界函数是整个定义域内都有界的函数,函数的单调性分为单调递增和单调递减。若函数在定义域内随着自变量x增大而值单调增大,则函数在该定义域内单调递增。函数的奇偶性描述了函数的对称性,奇函数为定义域关于原点对称的函数,偶函数为定义域关于y轴对称的函数,奇偶函数的定义域必关于原点对称,周期函数是一类特殊的函数,他以一定的周期不断重复。而奇函数和偶函数之间的加减乘除的结果也具有一定的规律性,奇函数加奇函数为奇函数,偶函数加偶函数为偶函数,奇函数与偶函数相乘为奇函数,偶函数与偶函数相乘为偶函数。
思维导图大纲
高等数学函数知识点思维导图模板大纲
定义
如果当变量x 在其变化范围内任意取定一个数值时,量y 按照一定的法则f 总有确 定的数值与它对应,则称y 是x 的函数。
变量x 的变化范围叫做这个函数的定义域。
通 常x 叫做自变量,y叫做函数值(或因变量),变量y 的变化范围叫做这个函数的值域。
函数相等
由函数的定义可知,一个函数的构成要素为:定义域、对应关系和值域
由于值域是由定义域和对应 关系决定的,所以,如果两个函数的定义域和对应关系完全一致,我们就称两个函数相等。
函数的简单性态
函数的有界性
如果对属于某一区间I 的所有x 值总有│f(x)│≤M 成立,其中M 是一个与x 无关 的常数,那么我们就称f(x)在区间I 有界,否则便称无界。
一个函数,如果在其整个定义域内有界,则称为有界函数。
函数的有界性,单调性应与相关点集联系起来,离开了点集。这些概念是没有任何意义的。
函数的单调性
如果函数在定义域区间(a,b)内随着x 增大而增大,即:对于(a,b)内任意两点x1 及x2,当x1<x2时,有,则称函数在区间(a,b)内是单调增加的。
如果函数在定义域区间(a,b)内随着x 增大而减小,即:对于(a,b)内任意两点x1 及x2,当x1<x2 时,有,则称函数在区间(a,b)内是单调减小的。
函数的奇偶性
函数的奇偶性
如果函数对于定义域内的任意x 都满足,则叫做偶函数;如果函数对于定义域内的任意x 都满足,则叫做奇函数。
偶函数的图形关于y 轴对称,奇函数的图形关于原点对称。
奇偶函数的定义域必关于原点对称。
函数的周期性
设的定义域为。若存在,对任意的,都使得,则称函数为周期函数,称为其周期。
奇函数+奇函数=奇函数
偶函数+偶函数=偶函数
奇函数·偶函数=奇函数
奇函数·奇函数=偶函数
偶函数·偶函数=偶函数
相关思维导图模板

树图思维导图提供 2021年陕西专升本高等数学考情分析 在线思维导图免费制作,点击“编辑”按钮,可对 2021年陕西专升本高等数学考情分析 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1d0caabbbed57665656478f48f0a0e24

















 上海工商
上海工商