数值微积分与方程求解思维导图
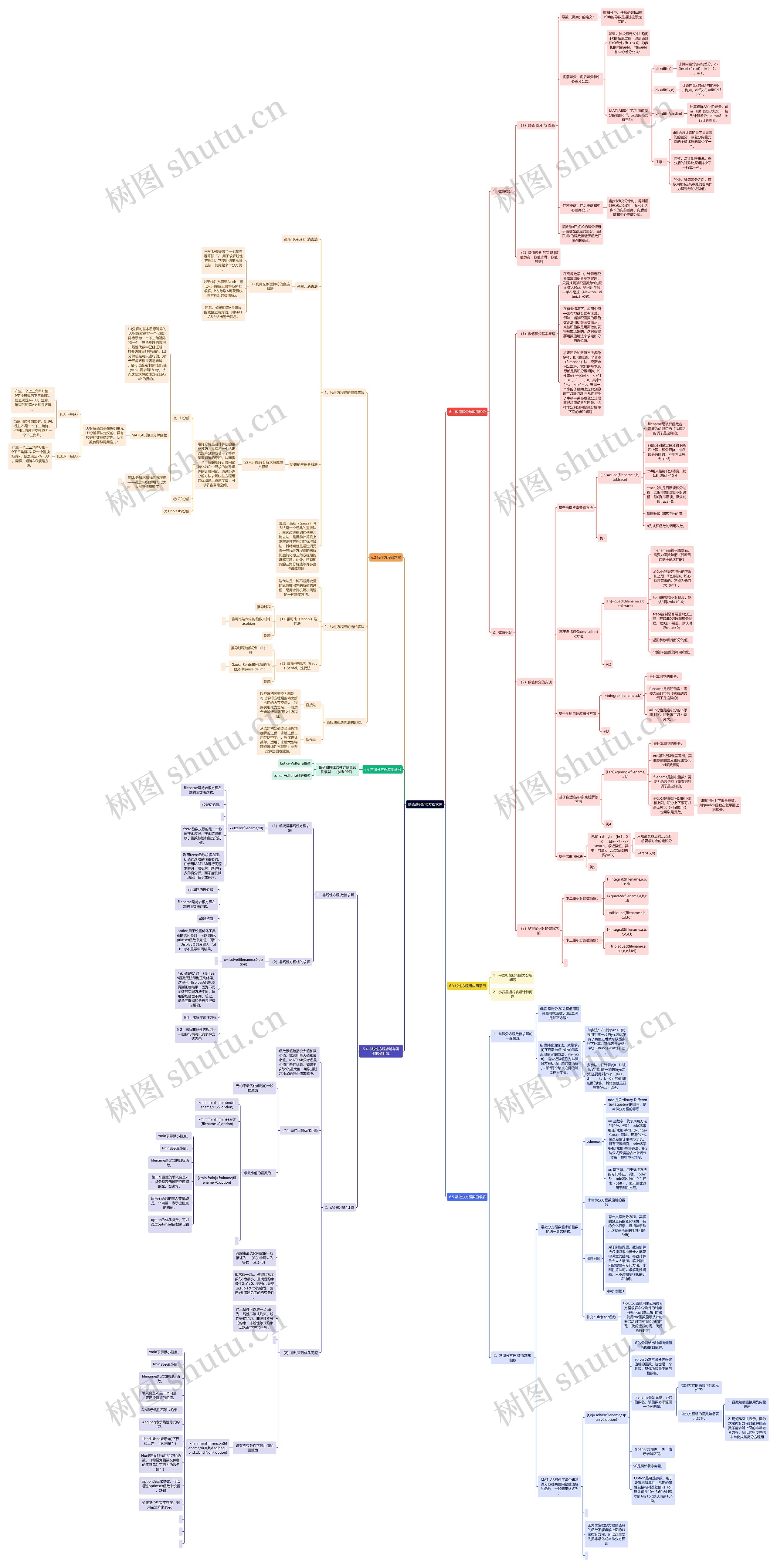
MATLAB数值微积分与方程求解
树图思维导图提供 数值微积分与方程求解 在线思维导图免费制作,点击“编辑”按钮,可对 数值微积分与方程求解 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ef20f25cc97e38927ac891456a150aa3
思维导图大纲
数值微积分与方程求解思维导图模板大纲
6.1 数值微分与数值积分
1.数值微分
(1)数值 差分 与 差商
导数(微商)的定义:
微积分中,任意函数f(x)在x0点的导数是通过极限定义的:
向前差分、向后差分和中心差分公式:
如果去掉极限定义中h趋向于0的极限过程,得到函数在x0点处以h(h>0)为步长的向前差分、向后差分和中心差分公式:
MATLAB提供了求 向前差分的函数diff,其调用格式有三种:
dx=diff(x)
计算向量x的向前差分,dx(i)=x(i+1)-x(i),i=1,2,…,n-1。
dx=diff(x,n)
计算向量x的n阶向前差分。例如,diff(x,2)=diff(diff(x))。
dx=diff(A,n,dim)
计算矩阵A的n阶差分,dim=1时(默认状态),按列计算差分;dim=2,按行计算差分。
注意:
diff函数计算的是向量元素间的差分,故差分向量元素的个数比原向量少了一个。
同样,对于矩阵来说,差分后的矩阵比原矩阵少了一行或一列。
另外,计算差分之后,可以用f(x)在某点处的差商作为其导数的近似值。
向前差商、向后差商和中心差商公式:
当步长h充分小时,得到函数在x0点处以h(h>0)为步长的向前差商、向后差商和中心差商公式:
函数f(x)在点x0的微分接近于函数在该点的差分,而f在点x的导数接近于函数在该点的差商。
(2)数值微分 的实现 [数值微商,数值求导,数值导数]
2.数值积分
(1)数值积分基本原理
在高等数学中,计算定积分依靠微积分基本定理,只要找到被积函数f(x)的原函数大F(x),则可用牛顿—莱布尼兹(Newton-Leibniz)公式:
在有些情况下,应用牛顿—莱布尼兹公式有困难,例如,当被积函数的原函数无法用初等函数表示,或被积函数是用离散的表格形式给出的。这时就需要用数值解法来求定积分的近似值。
求定积分的数值方法多种多样,如 梯形法、辛普森(Simpson)法、高斯求积公式等。它们的基本思想都是将积分区间[a,b]分成n个子区间[xi,xi+1],i=1,2,…,n,其中x1=a,xn+1=b,在每一个小的子区间上定积分的值可以近似求得,从而避免了牛顿—莱布尼兹公式需要寻求原函数的困难。这样求定积分问题就分解为下面的求和问题:
(2)数值积分的实现
基于自适应辛普森方法
[I,n]=quad(filename,a,b,tol,trace)
filename是被积函数名;需要为函数句柄(我看到的例子是这样的)
a和b分别是定积分的下限和上限,积分限[a,b]必须是有限的,不能为无穷大(Inf);
tol用来控制积分精度,默认时取tol=10-6;
trace控制是否展现积分过程,若取非0则展现积分过程,取0则不展现,默认时取trace=0;
返回参数I即定积分的值,
n为被积函数的调用次数。
例2
基于自适应Gauss-Lobatto方法
[I,n]=quadl(filename,a,b,tol,trace)
filename是被积函数名;需要为函数句柄(我看到的例子是这样的)
a和b分别是定积分的下限和上限,积分限[a,b]必须是有限的,不能为无穷大(Inf);
tol用来控制积分精度,默认时取tol=10-6;
trace控制是否展现积分过程,若取非0则展现积分过程,取0则不展现,默认时取trace=0;
返回参数I即定积分的值,
n为被积函数的调用次数。
例2
基于全局自适应积分方法
I=integral(filename,a,b)
I是计算得到的积分;
filename是被积函数;需要为函数句柄(我看到的例子是这样的)
a和b分别是定积分的下限和上限,积分限可以为无穷大。
例3
基于自适应高斯-克朗罗德方法
[I,err]=quadgk(filename,a,b)
I是计算得到的积分;
err返回近似误差范围,其他参数的含义和用法与quad函数相同。
filename是被积函数;需要为函数句柄(我看到的例子是这样的)
a和b分别是定积分的下限和上限,积分上下限可以是无穷大(−Inf或Inf),也可以是复数。
如果积分上下限是复数,则quadgk函数在复平面上求积分。
例4
基于梯形积分法
已知(xi,yi)(i=1,2,…,n),且a=x1<x2<…<xn=b,求近似值。其中,向量x、y定义函数关系y=f(x)。
只知道某些点的x,y坐标,想要求对应的定积分
I=trapz(x,y)
例5
(3)多重定积分的数值求解
求二重积分的数值解:
I=integral2(filename,a,b,c,d)
I=quad2d(filename,a,b,c,d)
I=dblquad(filename,a,b,c,d,tol)
求三重积分的数值解:
I=integral3(filename,a,b,c,d,e,f)
I=triplequad(filename,a,b,c,d,e,f,tol)
6.2 线性方程组求解
1.线性方程组的直接解法
高斯(Gauss)消去法
列主元消去法
(1) 利用左除运算符的直接解法
MATLAB提供了一个左除运算符“\”用于求解线性方程组,它使用列主元消去法,使用起来十分方便。
对于线性方程组Ax=b,可以利用左除运算符反斜杠求解,b左除以A可获得线性方程组的数值解x。
注意,如果矩阵A是奇异的或接近奇异的,则MATLAB会给出警告信息。
矩阵的三角分解法
(2) 利用矩阵分解求解线性方程组
矩阵分解是设计算法的重要技巧,是指将一个给定的矩阵分解成若干个特殊类型矩阵的乘积,从而将一个一般的矩阵计算问题转化为几个易求的特殊矩阵的计算问题。通过矩阵分解方法求解线性方程组的优点是运算速度快,可以节省存储空间。
① LU分解
LU分解的基本思想矩阵的LU分解就是将一个n阶矩阵表示为一个下三角矩阵和一个上三角矩阵的乘积。线性代数中已经证明,只要方阵是非奇异的,LU分解总是可以进行的。对于三角方程很容易求解,于是可以首先求解向量y使Ly=b,再求解Ux=y,从而达到求解线性方程组Ax=b的目的。
MATLAB的LU分解函数
LU分解函数是根据列主元LU分解算法定义的,具有较好的数据稳定性。lu函数有两种调用格式:
[L,U]=lu(A)
产生一个上三角阵U和一个变换形式的下三角阵L,使之满足A=LU。注意,这里的矩阵A必须是方阵。
当使用这种格式时,矩阵L往往不是一个下三角阵,但可以通过行交换成为一个下三角阵。
[L,U,P]=lu(A)
产生一个上三角阵U和一个下三角阵L以及一个置换矩阵P,使之满足PA=LU。同样,矩阵A必须是方阵。
用LU分解求解线性方程组——通过LU分解后可以大大提高运算速度
② QR分解
③ Cholesky分解
总结:高斯(Gauss)消去法是一个经典的直接法,由它改进得到的列主元消去法,是目前计算机上求解线性方程组的标准算法,其特点就是通过消元将一般线性方程组的求解问题转化为三角方程组的求解问题。此外,还有矩阵的三角分解法等许多直接求解算法。
2.线性方程组的迭代解法
迭代法是一种不断用变量的原值推出它的新值的过程,是用计算机解决问题的一种基本方法。
(1)雅可比(Jacobi)迭代法
推导过程
雅可比迭代法的函数文件jacobi.m:
例题
(2)高斯-赛德尔(Gauss-Serdel)迭代法
推导过程前部分和(1)一样
Gauss-Serdel迭代法的函数文件gauseidel.m:
例题
直接法和迭代法的比较:
直接法:
以矩阵初等变换为基础,可以求得方程组的精确解;占用的内存空间大、程序实现较为复杂;一般适合求解低阶稠密线性方程组。
迭代法:
从给定初始值逐步逼近精确解的过程,求解过程占用存储空间小,程序设计简单;适用于求解大型稀疏矩阵线性方程组;要考虑算法的收敛性。
6.3 线性方程组应用举例
1.平面桁架结构受力分析问题
2.小行星运行轨道计算问题
6.6 常微分方程应用举例
兔子和狐狸的种群数量变化模型:(参考PPT)
Lotka-Volterra模型
Lotka-Volterra改进模型
6.5 常微分方程数值求解
1.常微分方程数值求解的一般概念
求解 常微分方程 初值问题 就是寻找函数y(t)使之满足如下方程:
所谓其数值解法,就是求y(t)在离散结点tn处的函数近似值yn的方法,yn≈y(xn)。这些近似值称为常微分方程初值问题的数值解。相邻两个结点之间的距离称为步长。
单步法:在计算y(n+1)时只用到前一步的yn,因此在有了初值之后就可以逐步往下计算,其代表是龙格-库塔(Runge-Kutta)法。
多步法:在计算y(n+1)时,除了用到前一步的值yn之外,还要用到yn-p(p=1,2,…,k,k>0)的值,即前面的k步。其代表就是亚当斯(Adams)法。
2.常微分方程 数值求解 函数
常微分方程数值求解函数的统一命名格式:
odennxx
ode 是Ordinary Differential Equation的缩写,是常微分方程的意思。
nn 是数字,代表所用方法的阶数。例如,ode23采用2阶龙格-库塔(Runge-Kutta)算法,用3阶公式做误差估计来调节步长,具有低等精度。ode45采用4阶龙格-库塔算法,用5阶公式做误差估计来调节步长,具有中等精度。
xx 是字母,用于标注方法的专门特征。例如,ode15s、ode23s中的“s”代表(Stiff),表示函数适用于刚性方程。
求常微分方程数值解的函数
刚性问题
有一类常微分方程,其解的分量有的变化很快,有的变化很慢,且相差悬殊,这就是所谓的刚性问题(Stiff)。
对于刚性问题,数值解算法必须取很小步长才能获得满意的结果,导致计算量会大大增加。解决刚性问题需要有专门方法。非刚性算法可以求解刚性问题,只不过需要很长的计算时间。
参考 例题3
补充:tic和toc函数
tic和toc函数用来记录微分方程求解命令执行的时间,使用tic函数启动计时器,使用toc函数显示从计时器启动到当前所经历的时间。[代码运行时间,代码执行时间]
MATLAB提供了多个求常微分方程初值问题数值解的函数,一般调用格式为:
[t,y]=solver(filename,tspan,y0,option)
t和y分别给出时间向量和相应的数值解。
solver为求常微分方程数值解的函数。这也是一个参数,具体函数是不同的函数名。
filename是定义f(t,y)的函数名,该函数必须返回一个列向量。
微分方程的函数句柄表示如下:
微分方程组的函数句柄表示如下:
1. 函数句柄直接用列向量表示
2. 用矩阵乘法表示,因为求常微分方程数值解的函数不能求解上面的非常微分方程,所以这里要先把非常化成常微分方程组
tspan形式为[t0,tf],表示求解区间。
y0是初始状态向量。
Option是可选参数,用于设置求解属性,常用的属性包括相对误差值RelTol(默认值是10^-3)和绝对误差值AbsTol(默认值是10^-6)。
因为求常微分方程数值解的函数不能求解上面的非常微分方程,所以这里要先把非常化成常微分方程组
6.4 非线性方程求解与函数极值计算
1.非线性方程 数值求解
(1)单变量非线性方程求解
x=fzero(filename,x0)
filename是待求根方程左端的函数表达式,
x0是初始值。
fzero函数执行的是一个数值搜索过程,搜索结果依赖于函数特性和指定的初值。
利用fzero函数求解方程,初值的选取是很重要的。在使用MATLAB进行问题求解时,需要对问题进行多角度分析,而不能机械地套用命令或程序。
(2)非线性方程组的求解
x=fsolve(filename,x0,option)
x为返回的近似解,
filename是待求根方程左端的函数表达式,
x0是初值,
option用于设置优化工具箱的优化参数,可以调用optimset函数来完成。例如,Display参数设置为‘off’时不显示中间结果。
当初值是0.1时,利用fzero函数无法得到正确结果,这里利用fsolve函数就能得到正确结果,因为不同函数的实现方法不同,适用的场合也不同。总之,多角度选择和分析是很有必要的。
例1:求解非线性方程
例2:求解非线性方程组——函数句柄可以有多种方式表示
2.函数极值的计算
函数极值包括极大值和极小值,或者叫最大值和最小值。MATLAB只考虑最小值问题的计算,如果要求f(x)的最大值,可以通过求-f(x)的最小值来解决。
(1)无约束最优化问题
无约束最优化问题的一般描述为:
求最小值的函数为:
[xmin,fmin]=fminbnd(filename,x1,x2,option)
[xmin,fmin]=fminsearch(filename,x0,option)
[xmin,fmin]=fminunc(filename,x0,option)
xmin表示极小值点,
fmin表示最小值,
filename是定义的目标函数。
第一个函数的输入变量xl、x2分别表示被研究区间的左、右边界。
后两个函数的输入变量x0是一个向量,表示极值点的初值。
option为优化参数,可以通过optimset函数来设置。
(2)有约束最优化问题
有约束最优化问题的一般描述为:(G(x)也可以为等式:G(x)=0)
即求取一组x,使得目标函数f(x)为最小,且满足约束条件G(x)≤0。记号s.t.是英文subject to的缩写,表示x要满足后面的约束条件。
约束条件可以进一步细化为:线性不等式约束、线性等式约束、非线性不等式约束、非线性等式约束以及x的下界和上界。
求有约束条件下最小值的函数为:
[xmin,fmin]=fmincon(filename,x0,A,b,Aeq,beq,Lbnd,Ubnd,NonF,option)
xmin表示极小值点,
fmin表示最小值,
filename是定义的目标函数。
输入变量x0是一个向量,表示极值点的初值。
A,b表示线性不等式约束,
Aeq,beq表示线性等式约束,
Lbnd,Ubnd表示x的下界和上界,(列向量?)
NonF定义非线性约束的函数,(需要为函数文件名的字符串?可否为函数句柄?)
option为优化参数,可以通过optimset函数来设置。缺省
如果某个约束不存在,则用空矩阵来表示。
相关思维导图模板


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a

树图思维导图提供 第六章 群体传播与组织传播_副本 在线思维导图免费制作,点击“编辑”按钮,可对 第六章 群体传播与组织传播_副本 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1672f555831e7d9a3bb2cf2fb792cb49










 上海工商
上海工商