名师指导:数学分析学习方法详解思维导图

名师指导:数学分析学习方法详解思维导图,需要提高学习数学的兴趣,充分认识数学的重要性,并培养钻研的精神,要以知难而进的态度,面对学习数学难题,坚持不懈地继续学习,在学习数学分析时,需要注意其和高等数学的不同之处,注重分析能力的培养。要注意数学分析的系统性和连续性,学习扎实,否则将会影响后续学习和考研,使用思维导图可以帮助我们更好的理清思路,提高学习效率。
思维导图大纲
名师指导:数学分析学习方法详解思维导图模板大纲
名师指导:数学分析学习方法详解_名师指导
不经巨大的困难,不会有伟大的事业。对于攀登者来说,失掉往昔的足迹并不可惜,迷失了继续前时的方向却很危险。以下就是树图网为大家整理的名师指导:数学分析学习方法详解,一起来看看吧!希望能帮到大家。
名师指导:数学分析学习方法详解
1.提高学习数学的兴趣
首先要有学习数学的兴趣。两千多年前的孔子就说过:"知之者不如好之者,好之者不如乐之者。"这里的"好"与"乐"就是愿意学、喜欢学,就是学习兴趣,世界知名的伟大科学家、相对论学说的创立者爱因斯坦也说过:"在学校里和生活中,工作的最重要动机是工作中的乐趣。"学习的乐趣是学习的主动性和积极性,我们经常看到一些同学,为了弄清一个数学概念长时间埋头阅读和思考;为了解答一道数学习题而废寝忘食。这首先是因为他们对数学学习和研究感兴趣,很难想象,对数学毫无兴趣,见了数学题就头痛的人能够学好数学,要培养学习数学的兴趣首先要认识学习数学的重要性,数学被称为科学的皇后,它是学习科学知识和应用科学知识必须的工具。可以说,没有数学,也就不可能学好其他学科;其次必须有钻研的精神,有非学好不可的韧劲,在深入钻研的过程中,就可以领略到数学的奥妙,体会到学习数学获取成功的喜悦。长久下去,自然会对数学产生浓厚的兴趣,并激发出学好数学的高度自觉性和积极性。用兴趣推动学习,而不是用任务观点强迫自己被动地学习数学。
2.知难而进,迂回式学习
首先要培养学习数学分析的兴趣和积极性,还要不怕挫折,有勇气面对遇到的困难,有毅力坚持继续学习,这一点在刚开始进入大学学习数学分析时尤为重要。
中学数学和大学数学,由于理论体系的截然不同,使得同学们会在学习该课程开始阶段遇到不小的麻烦,这时就一定得坚持住,能够知难而进,继续跟随老师学习。
学习数学分析时要注意数学分析和高等数学要求不同的地方,否则你学习数学分析就与高等数学没有什么区别了;而且高等数学强调的是计算能力,数学分析强调的是分析的能力,分析的能力没有学到,就谈不上学好了数学分析。学好数学分析课程还有一个重要的原因是新生们体会不到的,数学分析的知识结构系统性和连续性很强,这些知识学得不扎实,肯定要影响后面知识的学习。同时将来考硕士,还是要考这门课程。如果大学第一年不把这门课程学好,将来可就难了。刚开始学习数学分析,会感觉很晕。对于老师所讲的知识,虽然表面上能听懂,但却不明白知识背后的真正原因,所以总是感觉学到的东西不实在。至于做题就更差劲了,课后习题都没几个会做的。其实感觉晕是很正常的,而且还得要晕上几个月才可能就会好的。所以要硬着头皮跟着老师学了下来。虽然感觉还是不太懂,虽然做作业仍然感觉很费劲,但始终不要放弃,这种状态是学习数学分析的一个必经之路,因此必须克服这个困难才能学好数学分析理论知识。
除了要坚持外,还要注意不要在某些问题的解决上花费过多的时间。因为数学分析理论十分严谨,教科书在讲解初步知识时,有时会不可避免地用到一些以后才能学到的理论思想,因而在初步学习时就对着这种问题不放是十分不划算的。比如说,在"数学分析"一开始学习实数系的确界存在基本定理时,由于当时根本没什么基础,所以对于"引入这个定理的目的是什么?"这个问题怎么想也想不通,甚至觉得这个定理没有什么实质的意义。但到后来学到了多元部分的数学分析,以及专业课"实变函数"时,才开始慢慢理解它的真正目的。这里之所以要说明是实数系有确界存在的性质,即相当于有一种连续的性质,目的就是为了后面的极限和连续做铺垫的,因为只有在自变量能够连续变化的时候,考虑因变量的相应变化才有意义,进而才能研究函数的性质。但是如果没有学到后面,只了解区间而不知其它一些怪异的点集时是很难想通这个问题的。
学习方法
二、有计划地安排学习,提高学习效率
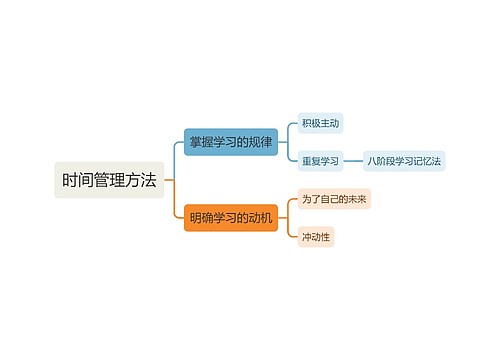
有些学生学习毫无计划,"脚踩西瓜皮,滑到哪里算到哪里",这是很不好的。高尔基说:"不知明天该做什么的人是不幸的。"学习也是这样,只有合理安排,明确学习目标,才能做到有的放矢,在学习上游刃有余。有的学生认为,学校有教育计划,老师有教学计划,跟着老师走,按照学校的要求办就行了,何必自己再定计划,这种想法是不对的。学校和老师的计划是针对全体学生的,每个学生还应该在老师要求的基础上,针对自己的学习情况制定出具体的个人学习计划。首先你要清楚一周内所要做的事情,然后制定一张作息时间表,在表上填上那些非花不可的时间,如:吃饭、睡觉、上课、运动、娱乐等。安排这些时间之后,选定合适的、固定的时间用来完成课后任务,当然,也要给休息、业余活动留出适当的时间,这对提高学习效率是非常有用的。
三、端正学习态度,找出适合自己的学习方法
我们不管干什么事情,一定要端正态度,要有一个良好的心态。学习是一项苦差事,在学习过程中我们会遇到很多困难,经常碰到学习上的"拦路虎",如果没有心理准备,没有好的心态,我们就很容易郁闷、烦躁甚至产生放弃学习的念头。因此,我们要保持平和的学习心态,本着获取知识、充实自己的目的去看待学习。学习需要认真和谦逊的态度,不认真的话,就会不严谨,容易疏漏一些知识点,也容易产生浮躁的心理;不谦逊的话,就会不思进取,自以为是,使知识面得不到进一步的拓展。有位哲人说过一句经典的话:态度决定一切。还有这样的话:做好做坏是能力问题,做与不做是态度问题。可见,正确的学习态度是非常重要的。
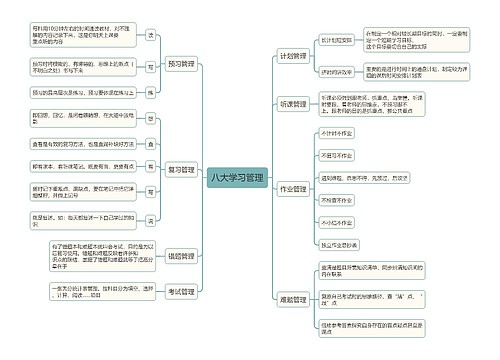
每一个学生都希望拥有一种适合自己的学习方法,原因是好的学习方法可以提高学习效率。当然,因人而异,每个人的思维方式和接受能力以及处事方式都是不同的,故适合其各自的学习方法也不尽相同。我国古代教育家曾提出过学习过程的"七步学习论",即立志(强调学习者对获取知识经验的动机、态度和目的)、博学(指阅读与获得信息)、审问、慎思、明辨、时习和笃行。我国现代教育工作者通过对学习过程结构的分析,明确提出了我国当代学生最优学习方法的八个环节,或叫"八环系统学习法",即"制订计划及执行学习计划的过程、课前自学、专心上课、及时复习、独立作业、解决疑难、系统小结和课外学习(包括阅读、参观访问、社会调查及科技活动等)"。上述八个环节在学生学习活动中的作用,不仅在于其促进学生对知识的学习与巩固,更重要的是能够满足和发展学生的学习兴趣和爱好的需要,激发其求知欲,培养他们的最佳学习心态及独立学习、分析和解决问题的能力。
以上是对大多数学生学习方法的总结和概括,不可能涵盖所有学习方法的内容。对于不同的大学生来说,这里面的有些方法是非常可取的,有些方法则是不合适的。有些学生喜欢博学却不喜欢审问、慎思;有些学生喜欢及时复习却不喜欢系统小结。所以,我们一定要根据各自的实际情况,找出真正适合我们的学习方法。
名师建议
在开始学习数学分析时,可以考虑采取迂回的学习方式。先把那些一时难以想通的问题记下,转而继续学习后续知识,然后不时地回头复习,在复习时由于后面知识的积累就可能会想通以前遗留的问题,进而又能促进后面知识的深刻理解。这种迂回式的学习方法,使得温故不但能知新,而且还能更好地知故。
但是,也并不是说在初学时就不去思考任何问题。相反,勤于思考是学好数学必备的好习惯,"数学是思维的体操",只有坚持思考才能掌握它的理论体系和逻辑关系。因此,应该在学习时掌握尺度,既要保证有充分的思考,但同时又不能过于钻牛角尖。
3.了解背景,理论式学习
数学分析与中学数学明显的一个差异就在于数学分析强调数学的基础理论体系,而中学数学则是注重计算与解题。针对这个特点,学习数学分析就应该注重建立自己的数学理论知识框架。
要学习理论体系,首先就应该知道为什么要建立这种理论,它的作用是什么,这就要了解数学的历史背景知识。比如"数学分析"在一开始就强调对?-N语言的掌握,而它的产生则是由于数学史上的"第二次数学危机"引起的。众所周知,Newton创立的微积分,虽然在其应用方面取得了巨大的成就,但微积分在那时的理论基础是相当混乱的。Newton在求导数时先将无穷小量看成非零数作为分母,后来又将其视做零而舍去,因此这就导致了逻辑上的错误。为了给微积分奠定正确而坚实的基础,大数学家威尔斯特拉森在Cauchy的基础上提出了用?-N语言的方法来推出极限和导数的概念。借助?-N语言,可以十分清晰地展示出函数取极限的过程,而且在逻辑上也非常清楚严谨。这样,当了解了这些历史背景知识之后,就觉得学习?-N语言是很必要的,学起来也就自然得多了。除了了解背景帮助我们学习理论知识外,还要下苦功夫去学习。在接触了这些陌生的数学理论一段时间后,可能觉得看起来已经懂了,但其实自己不一定能真正掌握,尤其是那些证明中内含的逻辑关系最容易出错。所以在学习时,应该适当地记忆理论知识,有时还应该默写定理,只有通过默写才能发现自己在理论上的漏洞,才能培养出自己严密的理论、逻辑能力,这对以后的学习都是很有帮助的。
相关思维导图模板
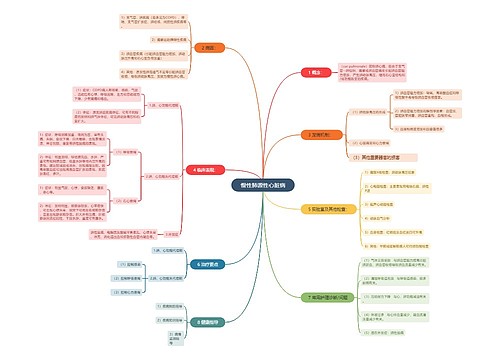

树图思维导图提供 慢性肺源性心脏病 在线思维导图免费制作,点击“编辑”按钮,可对 慢性肺源性心脏病 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d2393119f432b1d461ee990f7eefeb6a
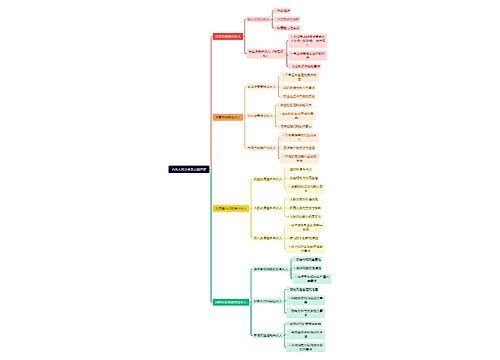

树图思维导图提供 合伙人的分类及功能详解 在线思维导图免费制作,点击“编辑”按钮,可对 合伙人的分类及功能详解 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a3379d96638da08b789972b795dd571e





 上海工商
上海工商