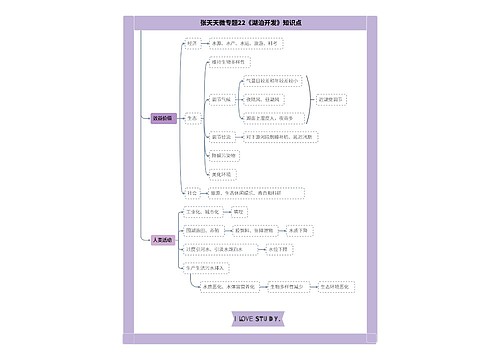
浙教版2018七年级数学上册期末试题附答案1(图形的初步知识)思维导图

本模板是一篇名为“浙教版2018七年级数学上册期末试题附答案1(图形的初步知识)思维导图”的思维导图模板,包含以下几个知识点,介绍几何图形的概念,区分立体图形和平面图形,和线段、射线和直线的概念,讲解线段、射线和直线的表示方法,数出图形中的线段、射线和直线,和线段的长短比较和简单的计算,教授用直尺和圆规画一条线段等于已知线段,介绍直线的基本事实,线段的基本事实及两点间距离的概念,讲解如何利用线段中点及线段和差关系求线段的长度,和如何运用“两点确定一条直线”、“两点之间线段最短”解决一些简单的实际问题,教授几何计数,通过练习题来帮助学生理解规律,计算能力和思考能力。
思维导图大纲
浙教版2018七年级数学上册期末试题附答案1(图形的初步知识)思维导图模板大纲
要求 知识与方法
了解 几何图形的概念,区分立体图形和平面图形
线段、射线和直线的概念
线段中点概念
理解 线段、射线和直线的表示方法,数出图形中的线段、射线和直线
线段的长短比较和简单的计算
用直尺和圆规画一条线段等于已知线段
直线的基本事实,线段的基本事实及两点间距离的概念
运用 利用线段中点及线段和差关系求线段的长度
运用"两点确定一条直线"、"两点之间线段最短"解决一些简单的实际问题
一、必备知识:
1.点、线、面、体称为____________.
2.经过两点____________一条直线.
3.线段有____________端点,它可以用表示它的____________端点的____________字母表示,也可以用一个____________字母表示.射线有____________端点,它可以用表示它的端点和射线上另外一个点的两个____________字母表示,表示端点的字母要写在____________.直线____________端点,它可以用它上面任意两个点的____________字母表示,也可以用一个____________字母表示.
4.在所有连结两点的线中,____________最短.连结两点的____________叫做两点间的距离.
二、防范点:
1.表示线段、直线时,注意区分大小写字母,小写字母一个就够,大写字母表示的话要两个字母,不要大小写字母一起用.射线的表示注意端点字母必在前.
2.两点间距离概念注意两个关键词,一个是"线段",一个是"长度",两者缺一不可.
几何图形
例1(1)如图,长方形绕它的一条边MN所在的直线旋转一周形成的几何体是()
(2)你能说出下面的图形中,哪些是平面图形,哪些是立体图形吗?
平面图形:________;立体图形:________.(填序号)
【反思】区分平面图形和立体图形往往看图形中有没有虚线.
直线、射线和线段
例2(1)如图所示,下面说法不正确的是()
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
(2)如图,图中有________条直线,它们是________,图中共有________条射线,它们中能用图中字母表示的有______________________________,图中共有________条线段,它们是____________________.
(3)如图,已知A,B,C,D四点,按要求画图:
①画线段AB,射线AD,直线AC;
②连结点B,D与直线AC交于点E;
③连结点B,C,并延长线段BC与射线AD交于点F.
【反思】数线段和射线主要看端点,线段看两个端点,射线看一个点,但数射线还应注意方向的不同.
直线和线段基本事实的应用
例3(1)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是__________________.
(2)如图,直线MN表示一条铁路,铁路两侧各有一个工厂,分别用A、B表示,现要在铁路边建立一个货物中转站,使中转站到两个工厂的距离之和最短,则这个中转站应建在什么位置?在图中标出来,并说明理由.
【反思】"两点确定一条直线","两点之间线段最短"这两个直线、线段的性质可以用来解释生活中很多现象,要正确区分两者的不同.
线段和差的计算
例4(1)如图,点C在线段AB上,点D是AC的中点,如果CD=3cm,AB=10cm,那么BC的长度是________cm.
(2)数轴上点A,B,C分别表示-2,4,8,则AC-BO(O为数轴的原点)=____________.
(3)已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,则线段AC=________.
(4)已知线段AB=2.4cm,点C在线段AB的延长线上,且AC=53BC,则线段BC的长度是________.
(5)如图,点B、C把线段AD分成2∶4∶3的三部分,M是AD的中点,CD=9,则线段MC的长度是________.
【反思】线段中点的知识常在求线段和差的问题中出现,要充分利用线段中点找寻线段之间的关系.如在求解过程中碰到比的关系往往可以用方程思想解决问题.
几何计数
例5(1)同一平面内有4条直线,那么这4条直线最多可以有多少个交点()
A.1 B.4 C.5 D.6
(2)数一数图中每个图形的线段总数:
图1中线段总数是________条;图2中线段总数是________条;图3中线段总数是________条;图4中线段总数是________条.
根据以上求线段的总数的规律:当线段上共有n个点(包括两个端点)时,线段的总数表示为________,利用以上规律,当n=22时,线段的总数是__________条.由以上规律,解答:如果10位同学聚会,互相握手致意,一共需要握多少次手?
【反思】解决几何计数问题,往往是从简单或特殊的情况入手,经过观察、猜想,发现规律.在考虑简单或特殊情况数个数的过程中常用"顺序数数法".
1.如图,C,B是线段AD上的两点,若AB=CD,BC=2AC,则AC与CD的关系为()
第1题图
A.CD=2AC B.CD=3AC C.CD=4AC D.不能确定
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 9.战斗的基督教 在线思维导图免费制作,点击“编辑”按钮,可对 9.战斗的基督教 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:33d168acd0cd9f767f809c7a5df86e3a












 上海工商
上海工商