高一数学教案:集合的含义及其表示思维导图
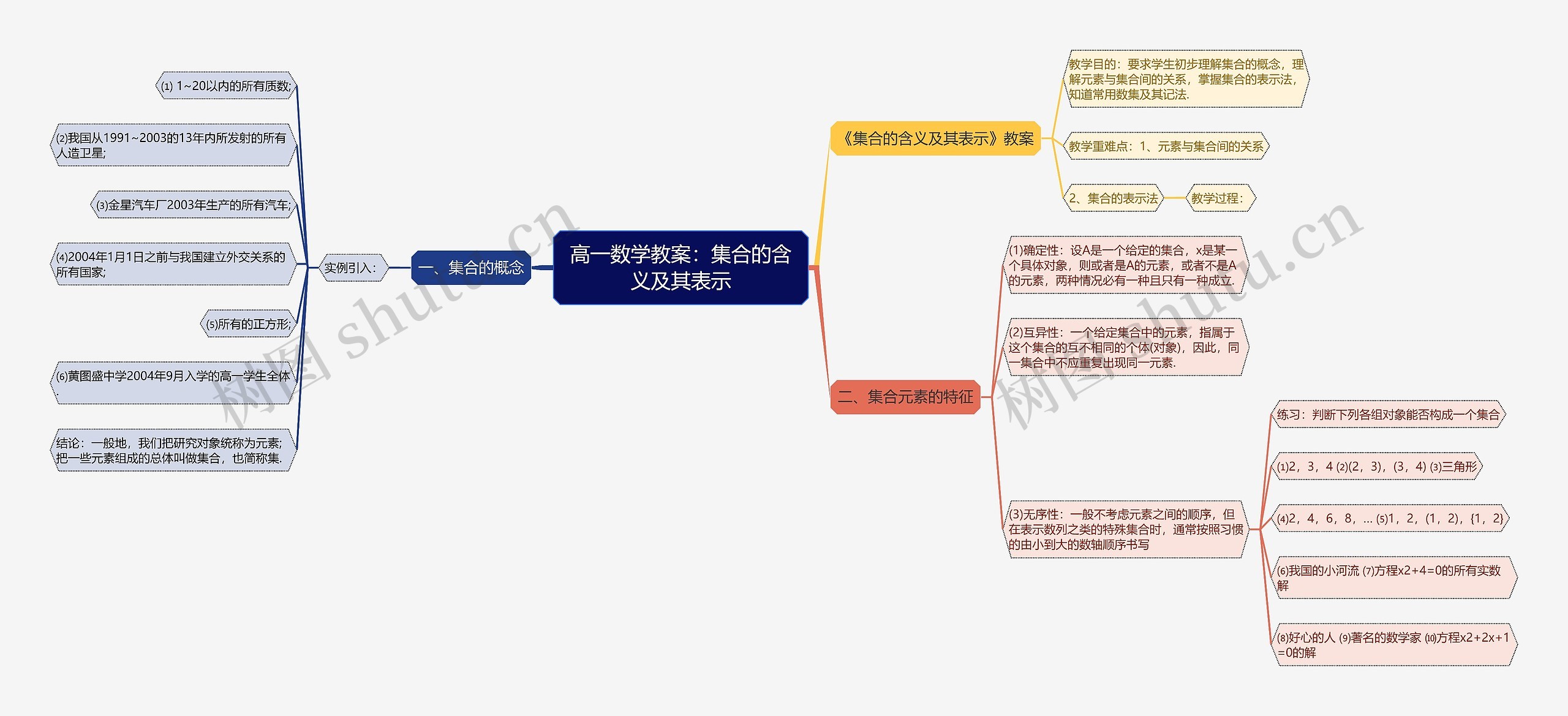
本“高一数学教案:集合的含义表示思维导图”包含如下知识点:1.集合/的概念:将研究对象统称为元素,将一些元素组成的总体称为集合。
2.集合/元素的特征:
-确定性:一个对象要么是集合的元素,要么不,且只有一种情况成立。
-互异性/:同一集合中的元素是互不相同的个体,不会重复出现。
-无序性:一般不考虑元素之间的顺序,但特殊集合如数列会按照从小到大的顺序书写。
教学过程中通过实例引入,让学生了解集合的具体用途,包含质数、人造卫星、汽车、国家、正方形和学生。之后学生需要判断一些对象是否能构成集合,进一步巩固对集合的理解。
简而言之,本教案教授了集合的含义、元素与集合的关系、集合的表示法和集合元素的特征。
思维导图大纲
高一数学教案:集合的含义及其表示思维导图模板大纲
《集合的含义及其表示》教案
教学目的:要求学生初步理解集合的概念,理解元素与集合间的关系,掌握集合的表示法,知道常用数集及其记法.
教学重难点:1、元素与集合间的关系
2、集合的表示法
教学过程:
一、集合的概念
实例引入:
⑴ 1~20以内的所有质数;
⑵我国从1991~2003的13年内所发射的所有人造卫星;
⑶金星汽车厂2003年生产的所有汽车;
⑷2004年1月1日之前与我国建立外交关系的所有国家;
⑸所有的正方形;
⑹黄图盛中学2004年9月入学的高一学生全体.
结论:一般地,我们把研究对象统称为元素;把一些元素组成的总体叫做集合,也简称集.
二、集合元素的特征
(1)确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立.
(2)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素.
(3)无序性:一般不考虑元素之间的顺序,但在表示数列之类的特殊集合时,通常按照习惯的由小到大的数轴顺序书写
练习:判断下列各组对象能否构成一个集合
⑴2,3,4 ⑵(2,3),(3,4) ⑶三角形
⑷2,4,6,8,… ⑸1,2,(1,2),{1,2}
⑹我国的小河流 ⑺方程x2+4=0的所有实数解
⑻好心的人 ⑼著名的数学家 ⑽方程x2+2x+1=0的解
相关思维导图模板

树图思维导图提供 高一数学教案:集合的含义及其表示(1) 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教案:集合的含义及其表示(1) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0b14c9e3572824a20e485ac7fe11b2f6

树图思维导图提供 高一数学教案:集合的含义及其表示(2) 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教案:集合的含义及其表示(2) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:adaecea28887abd202f9be064830727a








 上海工商
上海工商