高一数学教案:集合的含义及其表示(1)思维导图

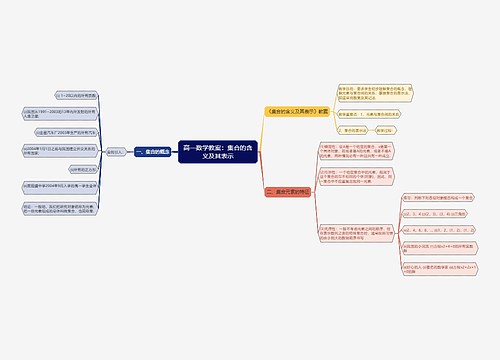
本高一数学教案的核心是集合的含义表示,教案包含以下知识点:1.教学/目标:初步理解集合的基本概念,了解“属于”关系的意义,常用数集的记法和集合中元素的特性,了解有限集、无限集、空集的概念。
2.教学/重点:集合概念和性质,“∈”和“Ï”的使用。
3.教学/难点:集合概念的理解。
4.引入课题:通过一个军训通知的例子引出集合的概念,解释集合即为研究对象的总体。
5.新课教学:介绍了物以类聚、人以群分的概念,和一些集合的例子,如自然数的集合,不等式的解集,和几何中的圆等。
6.元素/与集合的关系:介绍了元素属于集合的关系,用符号“∈”表示元素属于某个集合,用“Ï”表示元素不属于某个集合。
7.讨论/和点评:通过列举一些例子来判断是否构成集合,并提醒注意判断集合时范围的确定、元素的明确和能否指出集合的属性。
模板展示了高一数学教案中关于集合的含义表示的内容,帮助学生初步理解集合的概念和性质。
思维导图大纲
高一数学教案:集合的含义及其表示(1)思维导图模板大纲
集合的含义及其表示(1)
教学目标:使学生初步理解集合的基本概念,了解"属于"关系的意义、常用数集的记法和集合中元素的特性. 了解有限集、无限集、空集概念,
教学重点:集合概念、性质;"∈"," Ï"的使用
教学难点:集合概念的理解;
课 型:新授课
教学手段:
教学过程:
一、 引入课题
军训前学校通知:8月15日8点,高一年级在体育馆集合进行军训动员;试问这个通知的对象是全体的高一学生还是个别学生?
在这里,集合是我们常用的一个词语,我们感兴趣的是问题中某些特定(是高一而不是高二)对象的总体,而不是个别的对象,为此,我们将学习一个新的概念——集合(宣布课题),即是一些研究对象的总体。
研究集合的数学理论在现代数学中称为集合论,它不仅是数学的一个基本分支,在数学中占据一个极其独特的地位,如果把数学比作一座宏伟大厦,那么集合论就是这座宏伟大厦的基石。集合理论创始者是由德国数学家康托尔,他创造的集合论是近代许多数学分支的基础。(参看阅教材中读材料P17)。
下面几节课中,我们共同学习有关集合的一些基础知识,为以后数学的学习打下基础。
二、 新课教学
"物以类聚,人以群分"数学中也有类似的分类。
如:自然数的集合 0,1,2,3,……
如:2x-1>3,即x>2所有大于2的实数组成的集合称为这个不等式的解集。
如:几何中,圆是到定点的距离等于定长的点的集合。
1、一般地,指定的某些对象的全体称为集合,标记:A,B,C,D,…
集合中的每个对象叫做这个集合的元素,标记:a,b,c,d,…
2、元素与集合的关系
a是集合A的元素,就说a属于集合A, 记作 a∈A ,
a不是集合A的元素,就说a不属于集合A, 记作 aÏA
思考1:列举一些集合例子和不能构成集合的例子,对学生的例子予以讨论、点评,
进而讲解下面的问题。
例1:判断下列一组对象是否属于一个集合呢?
(1)小于10的质数(2)著名数学家(3)中国的直辖市(4)maths中的字母
(5)book中的字母(6)所有的偶数(7)所有直角三角形(8)满足3x-2>x+3的全体实数(9)方程 的实数解
评注:判断集合要注意有三点:范围是否确定;元素是否明确;能不能指出它的属性。
3、集合的中元素的三个特性:
1.元素的确定性:对于一个给定的集合,集合中的元素是确定的,任何一个对象或者是或者不是这个给定的集合的元素。
2.元素的互异性:任何一个给定的集合中,任何两个元素都是不同的对象,相同的对象归入一个集合时,仅算一个元素。比如:book中的字母构成的集合
3.元素的无序性:集合中的元素是平等的,没有先后顺序,因此判定两个集合是否一样,仅需比较它们的元素是否一样,不需考查排列顺序是否一样。
相关思维导图模板

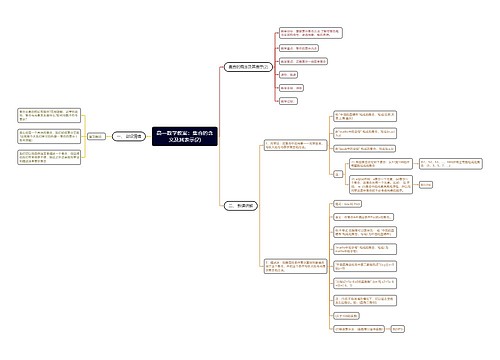
树图思维导图提供 高一数学教案:集合的含义及其表示 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教案:集合的含义及其表示 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c4ab322d0d7775e34babdd5530b4bcdc

树图思维导图提供 高一数学教案:集合的含义及其表示(2) 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教案:集合的含义及其表示(2) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:adaecea28887abd202f9be064830727a










 上海工商
上海工商