2022国考数量环形排列你还在出错?思维导图

在公务员考试中,排列组合往往是笔试考试中必不可少的一类题目,这一类题目难度居于行测数量关系前列,其中一部分原因就是大家容易忽视一些小细节,今天我们就来聊一聊排列组合中的环形排列。
树图思维导图提供 2022国考数量环形排列你还在出错? 在线思维导图免费制作,点击“编辑”按钮,可对 2022国考数量环形排列你还在出错? 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:d8cc5065659036088e14cf964c34a16b
思维导图大纲
2022国考数量环形排列你还在出错?思维导图模板大纲
在公务员考试中,排列组合往往是笔试考试中必不可少的一类题目,这一类题目难度居于行测数量关系前列,其中一部分原因就是大家容易忽视一些小细节,今天我们就来聊一聊排列组合中的环形排列。
一、环形排列解释
环形排列就是将要排列的对象在排列过程中围成一圈,在排列过程中不考虑东西南北的方位,只考虑要排列的元素的相对位置。
二、环形计算公式
环形排列不考虑方位,只考虑相对位置,如果我们有n个元素按照直线型去排列,那就重复了,大家想象一下,将所有的元素顺时针或者逆时针旋转,元素的相对位置同样没有发生变化,也就是产生了重复的情况,而重复的情况其实就是旋转引起的,n个元素每种情况都会出现n次,故用即可消除重复的情况,即n个元素环形排列公式为(种情况)。
三、例题练习
【例1】在一次同学聚会中,有5名同学围绕一张圆桌吃饭,请问这五名同学有多少种坐的方式?
A.20
B.60
C.24
D.12
【答案】C
【解析】第一步,本题考查排列组合,环形排列。
第二步,5名同学围绕圆桌坐下,圆桌故考虑本题考查环形排列,直接利用环形排列公式5个人环排,故情况数为(种)。
本题便是典型的环形排列问题,情况数直接套用环形排列公式即可得出结果。
四、环形排列忽视点
很多同学掌握了环形排列之后看到环形就使用公式去解决问题,这就导致出题人在设计坑的时候,很多同学容易入坑,选错选项。我们要明白环形排列之所以除以n,其实是为了消除重复的情况,但是有时候我们会遇到一些环形排列其实相对位置已经固定,那便不会产生重复。比如下面这个例题。
【例2】在一次同学聚会中有5名男同学和5名女同学围绕一圆桌就座,要求男生不能相邻,女生也不能相邻,那么共有()种不同坐法。
A. 480
B. 576
C. 600
D. 2880
【答案】D
【解析】第一步,本题考查排列组合,环形排列。
第二步,题目中要求男生不能相邻,女生也不能相邻,那么我们可以先排男生或者女生,再让另一个插空即可;先排的这个对象5个人圆桌故环形排列(种)。
第三步,5个人环形排列故产生5个空,此时虽然还是环形,但是这5个环形的座位周围都有了人,也就是任意一个人进任意一个空都是不同的,故不能再用环形排列而应该列式(种)。
第四步,故总情况数为24脳120=2880(种)。
五、小结
所以我们在做题中遇到环形排列时不仅要考虑去重复,同时也要清楚环形排列的原理是只考虑元素的相对位置,因此相对位置不同时,无需去除重复。希望同学们要掌握到这些技巧,早日成"公"。
相关思维导图模板


树图思维导图提供 熟悉商品(FamiliarizewithCommodities) 在线思维导图免费制作,点击“编辑”按钮,可对 熟悉商品(FamiliarizewithCommodities) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:dcfbd40001a21a643a50adc36a8f3741
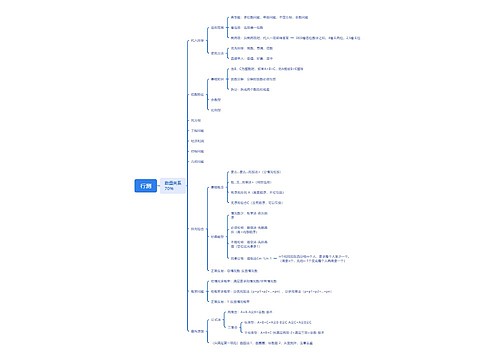

树图思维导图提供 行测数量关系 在线思维导图免费制作,点击“编辑”按钮,可对 行测数量关系 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0f7c9f8a68de14b47a5152799c0bea98

















 上海工商
上海工商