《高等数学》极限思维导图
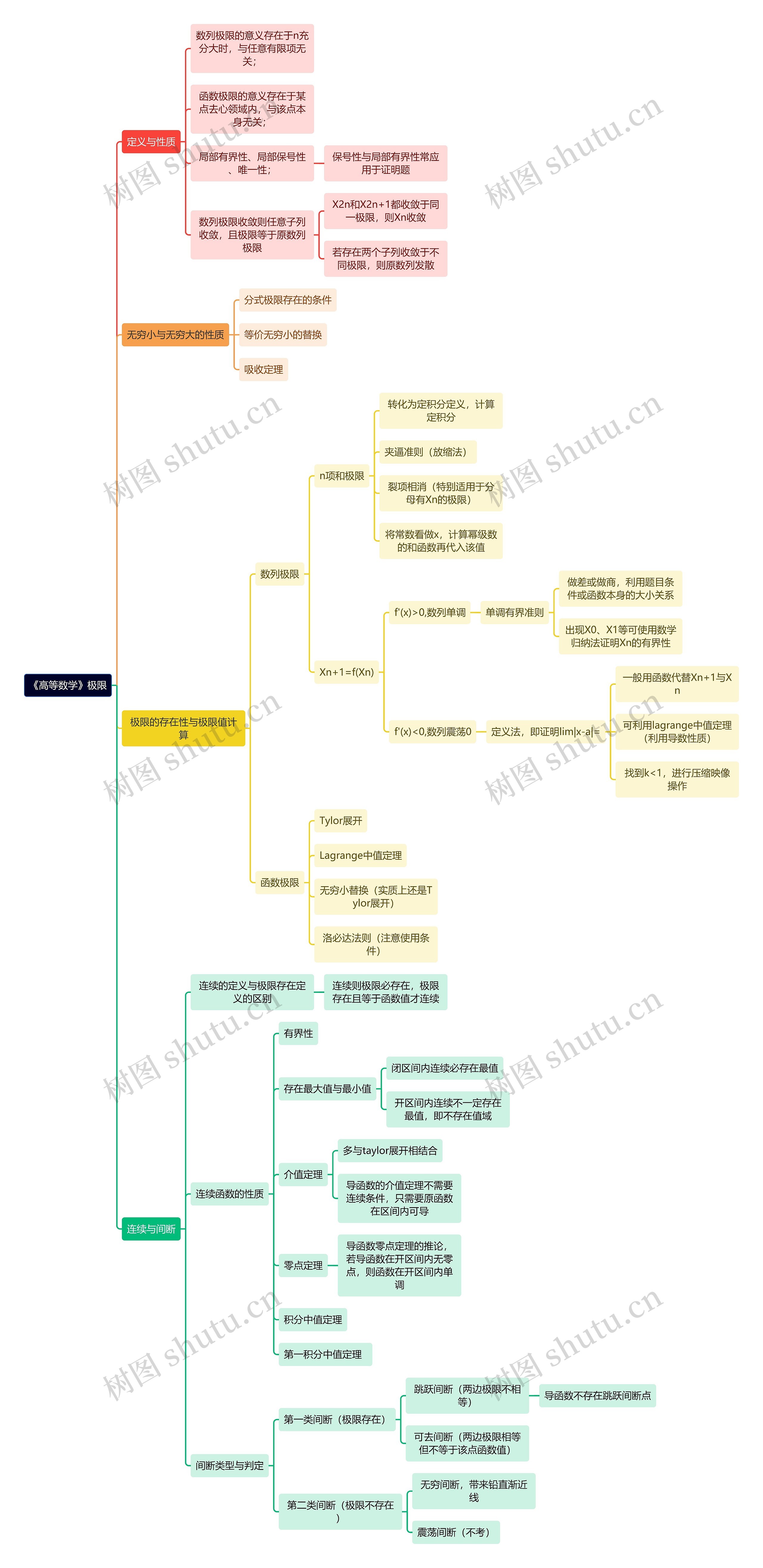
《高等数学》极限思维导图包含了数列极限、函数极限,数列极限存在于n充分大时,与任意有限项无关,而函数极限存在于某点去心领域内,与该点本身无关,局部有界性、局部保号性、唯一性对于证明题的保号性与局部有界性常应用。夹逼准则(放缩法)、裂项相消、连续函数的有界性知识点在计算极限值时很常见,导函数的介值定理、积分中值定理知识点可以用于求函数零点、证明函数的单调性,连续与间断也是该导图包含的一个重点。
思维导图大纲
《高等数学》极限思维导图模板大纲
定义与性质
数列极限的意义存在于n充分大时,与任意有限项无关;
函数极限的意义存在于某点去心领域内,与该点本身无关;
局部有界性、局部保号性、唯一性;
保号性与局部有界性常应用于证明题
数列极限收敛则任意子列收敛,且极限等于原数列极限
X2n和X2n+1都收敛于同一极限,则Xn收敛
若存在两个子列收敛于不同极限,则原数列发散
无穷小与无穷大的性质
分式极限存在的条件
等价无穷小的替换
吸收定理
极限的存在性与极限值计算
数列极限
n项和极限
转化为定积分定义,计算定积分
夹逼准则(放缩法)
裂项相消(特别适用于分母有Xn的极限)
将常数看做x,计算幂级数的和函数再代入该值
Xn+1=f(Xn)
f'(x)>0,数列单调
单调有界准则
做差或做商,利用题目条件或函数本身的大小关系
出现X0、X1等可使用数学归纳法证明Xn的有界性
f'(x)<0,数列震荡0
定义法,即证明lim|x-a|=
一般用函数代替Xn+1与Xn
可利用lagrange中值定理(利用导数性质)
找到k<1,进行压缩映像操作
函数极限
Tylor展开
Lagrange中值定理
无穷小替换(实质上还是Tylor展开)
洛必达法则(注意使用条件)
连续与间断
连续的定义与极限存在定义的区别
连续则极限必存在,极限存在且等于函数值才连续
连续函数的性质
有界性
存在最大值与最小值
闭区间内连续必存在最值
开区间内连续不一定存在最值,即不存在值域
介值定理
多与taylor展开相结合
导函数的介值定理不需要连续条件,只需要原函数在区间内可导
零点定理
导函数零点定理的推论,若导函数在开区间内无零点,则函数在开区间内单调
积分中值定理
第一积分中值定理
间断类型与判定
第一类间断(极限存在)
跳跃间断(两边极限不相等)
导函数不存在跳跃间断点
可去间断(两边极限相等但不等于该点函数值)
第二类间断(极限不存在)
无穷间断,带来铅直渐近线
震荡间断(不考)
相关思维导图模板
树图思维导图提供 高等数学-极限 在线思维导图免费制作,点击“编辑”按钮,可对 高等数学-极限 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:532e3295c206a4714de699ea1d05128d

















 上海工商
上海工商