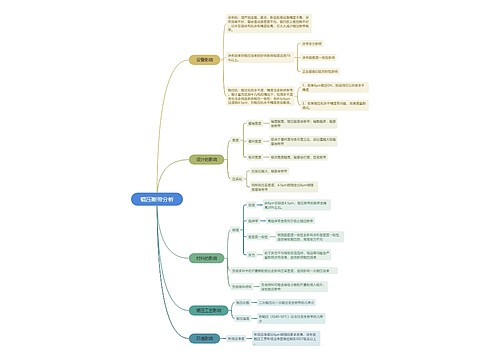
描述分析思维导图

我们学习“概率和统计学”目的在于应用到对于“对象”的研究中

笔者将我们要研究的“对象”按照维度分为了两大类

一维：就是当前摆在我们面前的“一组”，“一批”，哪怕是“一坨”数据

这里我们会用到统计学的知识去研究这类对象

二维：就是研究某个“事件”，笔者认为事件是依托于“时间轴”存在的，过去是否发生

现在是可能会出现几种情况，每种情况未来发生的可能性有多大？

这类问题是属于概率论的范畴。因此，我们在做数据分析的研究前

一般是面容怎么样？身段怎么样？两个维度去描述。就像画一幅肖像画

“集中趋势---代表值”，“分散和程度”。

至于从哪些特征开始说呢？就是常用的概念“均值”，“方差”之类的

数据分析中最常规的情况，比如你手上有一组，一批或者一坨数据

通常可以从两个维度去描述：集中趋势量度：为这批数据找到它们的“代表”均值（μ）

均值的局限性均值是最常用的平均数之一，但是它的局限性在于

“若用均值描述的数据中存在异常值的情况，会产生偏差”

中位数中位数，又称中点数，中值。是按顺序排列的一组数据中居于中间位置的数

众数众数是样本观测值在频数分布表中频数最多的那一组的组中值

平均数可以表征一批数据的典型值，但是仅凭平均数还不能给我们提供足够的信息

平均数无法表征一组数据的分散程度

全距也叫“极差”极差。它是一组数据中最大值与最小值之差

可以用于度量数据的分散程度。全距的局限性全距虽然求解方便快捷

但是它的局限性在于“若数据中存在异常值的情况，会产生偏差

四分位数所有观测值从小到大排序后四等分，处于三个分割点位置的数值就是四分位数

“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字

又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字。

又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

如果出现了极大或极小的异常值，将会被排除在中心数据50%以外

因此使用迷你距可以剔除数据中异常值。全距，四分位距

箱形图可以表征一组数据极大和极小值之间的差值跨度，一定程度上反应了数据的分散程度

但是却无法精准的告诉我们，这些数值具体出现的频率，那么我们该如何表征呢

我们度量每批数据中数值的“变异”程度时，可以通过观察每个数据与均值的距离来确定

各个数值与均值距离越小，变异性越小数据越集中，距离越大数据约分散，变异性越大

方差和标准差就是这么一对儿用于表征数据变异程度的概念

方差方差是度量数据分散性的一种方法，是数值与均值的距离的平方数的平均值

标准差标准差为方差的开方标准分——表征了距离均值的标准差的个数

通过方差和标准差我们现在可以表征一组数据的数值的变异程度

那么对于拥有不同均值和不同标准差的多个数据集我们如何比较呢

标准分为我们提供了解决方法，当比较均值和标准差各不相同的数据集时

我们可以把这些数值视为来自同一个标准的数据集，然后进行比较

标准分将把每一个数据集转化为通用的分布形态，进行比较

标准分还有个重要的作用它可以把正态分布变为标准正态分布

通过分散和变异性的描述，查看这批数据的分散程度

集中趋势参数：均值，中位数，众数

分散性和变异性参数 : 全距，四分位距，方差，标准差，标准分